Đáp án C
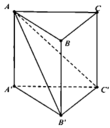
Ta có
B C ⊥ A C , B C ⊥ A A ' ⇒ B C ⊥ A ' A C C ' ⇒ B C ⊥ A ' C .
Suy ra
A ' C B , A B C ^ = A ' C , A C ^ = A ' C A ^ = x , 0 < x < π 2 .
Δ A ' A C vuông tại B nên
A A ' = A ' C . sin A ' C A ^ = a sin x ; A C = a cos x .
Suy ra
V A ' . A B C = 1 3 . A A ' . S Δ A B C = 1 3 . a sin x . a cos x 2 2 = a 3 6 sin x cos 2 x .
Xét hàm số
f x = sin x cos 2 x = sin x 1 − sin 2 x trên 0 ; π 2 .
Đặt t = sin x , do x ∈ 0 ; π 2 ⇒ t ∈ 0 ; 1 . Xét hàm số g t = t 1 − t 2 trên 0 ; 1 .
Ta có
f ' t = 1 − 3 t 2 ; f ' t = 0 ⇔ t = ± 1 3 .
Do t ∈ 0 ; 1 nên t = 1 3 .
Lập bảng biến thiên, suy ra max x ∈ 0 ; π 2 f x = max t ∈ 0 ; 1 g t = g 1 3 = 2 3 9 .
Vậy V max = a 3 6 . 2 3 9 = a 3 3 27 (đvtt).