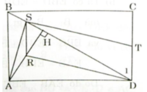
a) Hai tam giác vuông AHD và BDC có ∠ADH = ∠CBD (SLT)
⇒ ΔAHD ∼ ΔDCB (g.g)
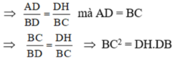
b) Ta có S, R là trung điểm của HB và AH nên SR là đường trung bình của ΔABH ⇒ SR // AB
⇒ ∠HSR = ∠HBA (đồng vị)
Mà ∠HBA = ∠D1
⇒ HSR = ∠D1
Do đó ΔSHR ∼ ΔDCB (g.g)
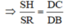
![]()
c) Ta có SR // AB và SR = AB/2 (cmt), TD = CD/2
mà AB = CD và AB // CD (gt)
⇒ SR // DT và SR = DT
Do đó Tứ giác DRST là hình bình hành
d) Ta có SR // AB mà AB ⊥ AD (gt) ⇒ SR ⊥ AD, lại có AH ⊥ SD (gt)
⇒ R là trực tâm của ΔSAD ⇒ DR là đường cao thứ ba nên DR ⊥ SA
Mà DR // ST (DRST là hình bình hành) ⇒ ST ⊥ SA
Vậy ∠AST = 90o

