Question

Cho hình chữ nhật ABCD. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA.

a)EFGH là hình gì? Vì sao?

b) Chứng minh AC, BD, EG, FH đồng qui

Answer 1

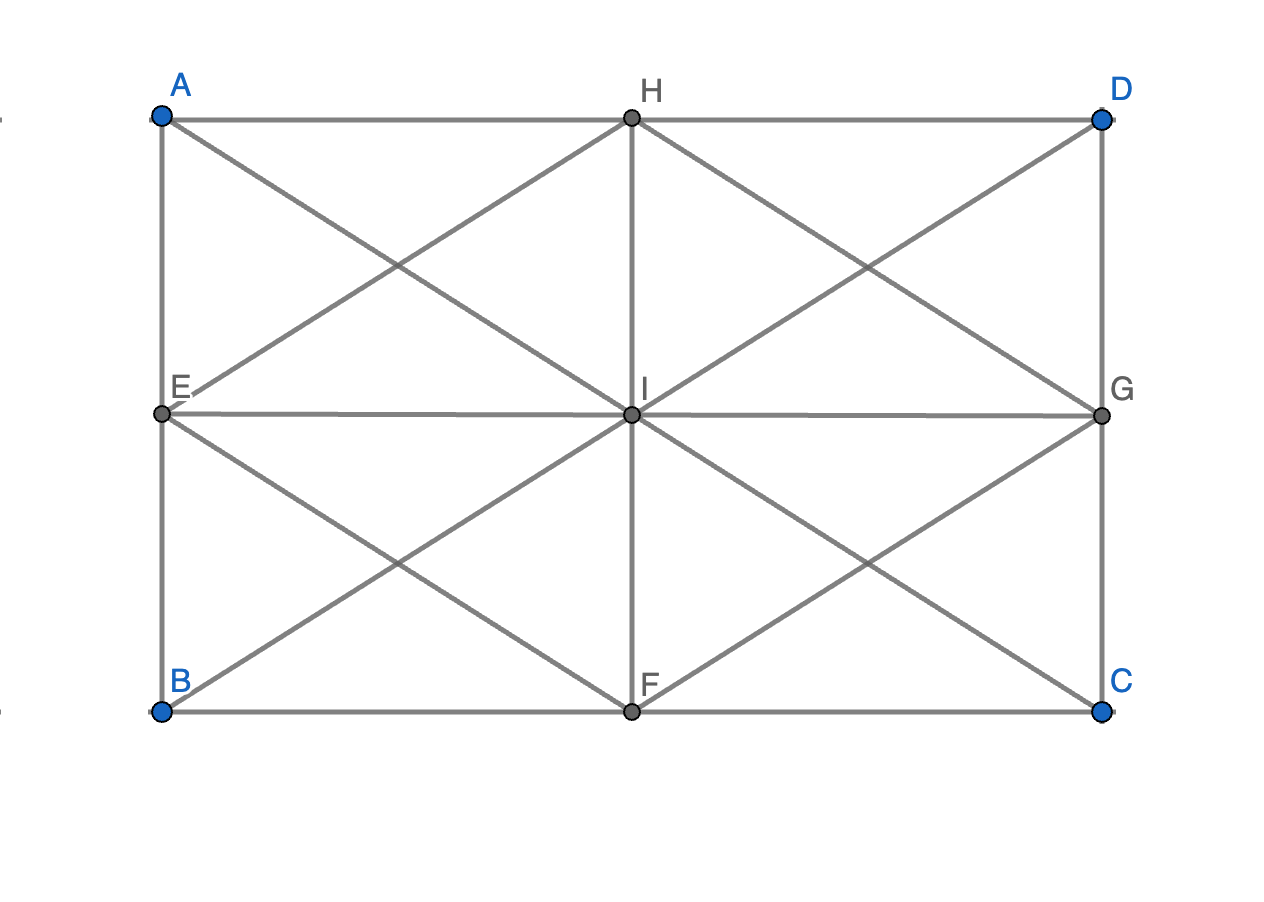
a) Ta có: E là trung điểm AB, F là trung điểm BC

=> EF là đường trung bình \(\Delta ABC\)

=> \(\)EF // AC và EF = AC/2

Tương tự với các  \(\Delta ADC\), ABD, BCD

=> HG // AC và HG = AC/2, EH // BD và EH = BD/2, FG // BD và FG = BD/2

Mà ABCD là hình chữ nhật => AC = BD => EF = HG = FG = EH

Tứ giác EFGH có 4 cạnh bằng nhau => EFGH là hình thoi

b) ABCD là hình chữ nhật => AC, BD cắt nhau tại trung điểm mỗi đường (1)

EFGH là hình thoi => EG, FH cắt nhau tại trung điểm mỗi đường (2)

Ta thấy AH // CF và AH = CF = AD/2 => AHCF là hình bình hành => AC, HF cắt nhau tại trung điểm mỗi đường (3)

Từ (1), (2), (3) => AC, BD, EG, FH đồng quy tại điểm I là trung điểm mỗi đường.

 

Answer 2