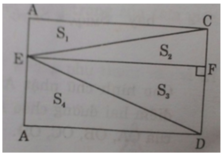
Kẻ EF ⊥ CD ⇒ AC // EF // AD
Xét ΔBCE và ΔFEC có:
(CAE) = (CFE) = 90o
(BCE) = (CEF) (Hai góc so le trong)
CE chung
⇒ ΔBCE = ΔFEC (cạnh huyền- góc nhọn)
tương tự ΔAED=ΔFDE.
Do đó (theo hình vẽ):
S1 = S2 và S3 = S4
⇒ S2 + S3 = S1 + S4 = (1/2)SABCD
Hay SECD = (1/2)SABCD ⇒ SABCD = 2SECD.

