Đáp án A
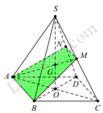
Gọi G là trọng tâm của tam giác SAC và AG cắt SC tại M =>M là trung điểm của SC, tương tự N là trung điểm của SD. Do đó, mp (P) cắt khối chóp theo thiết diện là tứ giác ABMN.
Ta có
V S . A M N V S . A C D = S M S C . S N S D = 1 4 ; V S . A B M V S . A B C = 1 2 ⇒ V S . A B M N V S . A B C D = 3 8 .
Suy ra
V S . A B M N = 3 8 . 1 3 . S O . S A B C D = a 8 . tan 60 ∘ . 2 a 2 = a 3 3 2 .
Cho hình chóp đều S.ABCD, có cạnh đáy bằng 2a. Mặt bên hình chóp tạo với đáy một góc bằng 60 ° . Mặt phẳng (P) chứa AB đi qua trọng tâm G của tam giác SAC cắt SC, SD lần lượt tại M, N. Tính theo a thể tích V khối chóp S.ABMN
A. V = 3 a 3
B. V = 3 4 a 3
C. V = 3 2 a 3
D. 3 3 2 a 3
Cho hình chóp đều S.ABCD có độ dài cạnh đáy bằng a. Gọi G là trọng tâm tam giác SAC . Mặt phẳng chứa AB và đi qua G cắt các cạnh SC, SD lần lượt tại M và N. Biết mặt bên của hình chóp tạo với đáy một góc bằng 60 ° . Thể tích khối chóp S.ABMN bằng
A. a 3 3 4
B. a 3 3 8
C. a 3 3 16
D. 3 a 3 3 16
Cho hình chóp tứ giác đều S.ABCD, đáy là hình vuông cạnh a, cạnh bên tạo với góc 60 ° . Gọi M là trung điểm của SC. Mặt phẳng qua AM và song song với BD, cắt SB, SD lần lượt tại E và F và chia khối chóp thành hai phần. Tính thể tích V của khối chóp không chứa đỉnh S.
A. V = a 3 6 36
B. V = a 3 6 9
C. V = a 3 6 18
D. V = a 3 6 12
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D. SA vuông góc với mặt phẳng đáy (ABCD); AB=2a; AC=CD=a. Mặt phẳng (P) đi qua CD và trọng tâm G của tam giác SAB cắt các cạnh SA, SB lần lượt tại M và N. Tính thể tích khối chóp S.CDMN theo thể tích khối chóp S.ABCD
A. V S . C D M N = 14 27 V S . A B C D
B. V S . C D M N = 4 27 V S . A B C D
C. V S . C D M N = 10 27 V S . A B C D
D. V S . C D M N = 1 2 V S . A B C D
Cho hình chóp S.ABCD có đáy là hình vuông cạnh cạnh 2 2 bên SA vuông góc với mặt phẳng đáy và SA = 3 Mặt phẳng qua A và vuông góc với SC cắt cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Thể tích V của khối cầu ngoại tiếp tứ diện CMNP
A. V = 125 π 6
B. V = 32 π 3
C. V = 108 π 3
D. V = 64 2 π 3
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên tạo với đáy một góc 60 o . Gọi M là trung điểm của SC. Mặt phẳng đi qua AM và song song với BD cắt SB tại E và cắt SD tại F. Tính thể tích V khối chóp S.AEMF.
A. V = a 3 6 36 .
B. V = a 3 6 9 .
C. V = a 3 6 6 .
D. V = a 3 6 18 .
Hình chóp tứ giác đều S.ABCD có cạnh đáy có độ dài a. Mặt phẳng (P) qua A và vuông góc với SC cắt SB, SC, SD lần lượt tại B’, C’, D’ sao cho S B ' = 2 B B ' Tỉ số giữa thể tích hình chóp S.AB’C’D’ và thể tích hình chóp S.ABCD bằng
A. 2 3
B. 4 9
C. 1 3
D. 4 27
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân ở B, A C = a 2 . SA vuông góc với mặt phẳng (ABC) và (SA)=a. Gọi G là trọng tâm của tam giác SBC. Một mặt phẳng đi qua hai điểm A, G và song song với BC cắt SB, SC lần lượt tại B’ và C’. Thể tích khối chóp S.A’B’C’ bằng:
A. 2 a 3 9
B. 2 a 3 27
C. a 3 9
D. 4 a 3 27
Cho khối chóp S.ABCD có đáy là hình bình hành. (P) là mặt phẳng chứa AB, cắt SC, SD tại M, N sao cho SM = 1/3. SC. Gọi V1, V2 lần lượt là thể tích khối chóp S.ABMN và khối đa diện ABCDNM. Khi đó tỉ số V1/ V2 bằng:
A. 2/7
B. 2/9
C. 1/2
D. 1/8
