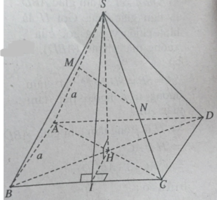
a) (AC ⊥ SH & AC ⊥ BD ⇒ AC ⊥ (SBD) ⇒ AC ⊥ SD.
b) (MN//AC & AC ⊥ (SBD) ⇒ MN ⊥ (SBD).
c) + Xác định góc α giữa (SBC) và (ABCD)
Gọi I là trung điểm của BC, ta có:
(BC ⊥ IH & BC ⊥ SH ⇒ BC ⊥ (SIH)
⇒ BC ⊥ SI.
⇒ [((SBC),(ABCD)) ] = ∠(SIH) = α.
+ Tính α:
Trong tam giác SIH, ta có: cosα = IH/IS = √3/3 ⇒ α = arccos√3/3.

