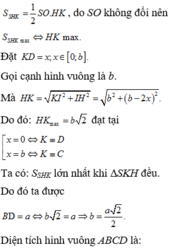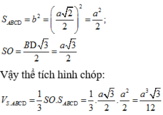Các câu hỏi tương tự
Cho khối chóp tứ giác đều S.ABCD, gọi
α
mặt phẳng qua A và vuông góc SC. Biết rằng diện tích thiết diện tạo bởi
α
là hình chóp bằng nửa diện tích đáy ABCD. Tínhgóc
φ
tạo bởi cạnh bên SC và mặt đáy. A.
φ
arcsin
1
+
33
8
B.
φ
arcsin
33...
Đọc tiếp
Cho khối chóp tứ giác đều S.ABCD, gọi α mặt phẳng qua A và vuông góc SC.
Biết rằng diện tích thiết diện tạo bởi α là hình chóp bằng nửa diện tích đáy ABCD. Tính
góc φ tạo bởi cạnh bên SC và mặt đáy.
A. φ = arcsin 1 + 33 8
B. φ = arcsin 33 − 1 8
C. φ = arcsin 1 + 29 8
D. φ = arcsin 29 − 1 8
Cho hình chóp đều S.ABCD có tất cả các cạnh bằng a, điểm K thuộc cạnh SC sao cho SK2KC. Mặt phẳng (P) chứa AK và song song BD. Tính diện tích của thiết diện của hình chóp S.ABCD cắt bởi (P). A.
3
a
2
5
B.
2
26
a...
Đọc tiếp
Cho hình chóp đều S.ABCD có tất cả các cạnh bằng a, điểm K thuộc cạnh SC sao cho SK=2KC. Mặt phẳng (P) chứa AK và song song BD. Tính diện tích của thiết diện của hình chóp S.ABCD cắt bởi (P).
A. 3 a 2 5
B. 2 26 a 2 15
C. 4 26 a 2 15
D. 2 3 a 2 5
Cho hình chóp đều S.ABCD có tất cả các cạnh bằng a, điểm M thuộc cạnh SC sao cho
S
M
2
M
C
. Mặt phẳng (P)chứa AM và song song với BD. Tính diện tích thiết diện của hình chóp S.ABCD cắt bởi (P). A.
3
a
2
5
B.
4
26...
Đọc tiếp
Cho hình chóp đều S.ABCD có tất cả các cạnh bằng a, điểm M thuộc cạnh SC sao cho S M = 2 M C . Mặt phẳng (P)chứa AM và song song với BD. Tính diện tích thiết diện của hình chóp S.ABCD cắt bởi (P).
A. 3 a 2 5
B. 4 26 a 2 15
C. 2 26 a 2 15
D. 2 3 a 2 5
Một viên đá có hình dạng là khối chóp tứ giác đều với tất cả các cạnh bằng a. Người ta cắt khối đá đó bởi mặt phẳng song song với đáy của khối chóp để chia khối đá thành hai phần có thể tích bằng nhau. Tính diện tích của thiết diện khối đá bị cắt bởi mặt phẳng nói trên. (Giả thiết rằng tổng thể tích của hai khối đá sau vẫn bằng thể tích của khối đá ban đầu). A.
2
a
2
3...
Đọc tiếp
Một viên đá có hình dạng là khối chóp tứ giác đều với tất cả các cạnh bằng a. Người ta cắt khối đá đó bởi mặt phẳng song song với đáy của khối chóp để chia khối đá thành hai phần có thể tích bằng nhau. Tính diện tích của thiết diện khối đá bị cắt bởi mặt phẳng nói trên. (Giả thiết rằng tổng thể tích của hai khối đá sau vẫn bằng thể tích của khối đá ban đầu).
A. 2 a 2 3
B. a 2 2 3
C. a 2 4
D. a 2 4 3
Cho khối đa diện như hình vẽ bên. Trong đó ABC.A B C là khối lăng trụ tam giác đều có tất cả các cạnh đều bằng 1, S.ABC khối chóp tam giác đều có cạnh bên SA2/3. Mặt phẳng (SA B ) chia khối đa diện đã cho thành hai phần. Gọi
V
1
là thể tích phần khối đa diện chứa đỉnh A,
V
2
là thể tích phần khối đa diện không chứa đỉnh A. Mệnh đề nào sau đây đúng A.
72
V
1...
Đọc tiếp
Cho khối đa diện như hình vẽ bên. Trong đó ABC.A' B' C' là khối lăng trụ tam giác đều có tất cả các cạnh đều bằng 1, S.ABC khối chóp tam giác đều có cạnh bên SA=2/3. Mặt phẳng (SA' B' ) chia khối đa diện đã cho thành hai phần. Gọi V 1 là thể tích phần khối đa diện chứa đỉnh A, V 2 là thể tích phần khối đa diện không chứa đỉnh A. Mệnh đề nào sau đây đúng
A. 72 V 1 = 5 V 2
B. 3 V 1 = V 2
C. 24 V 1 = 5 V 2
D. 4 V 1 = 5 V 2
Cho hình chóp A.BCD có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A trên mặt phẳng đáy là trung điểm H của CD. Cắt hình chóp bởi mặt phẳng
(
α
)
song song với AB và CD. Tính diện tích S của thiết diện thu được, biết
d
(
B
,
(
α
)
)
a
2
,
A
B
a
2
A. ...
Đọc tiếp
Cho hình chóp A.BCD có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A trên mặt phẳng đáy là trung điểm H của CD. Cắt hình chóp bởi mặt phẳng ( α ) song song với AB và CD. Tính diện tích S của thiết diện thu được, biết d ( B , ( α ) ) = a 2 , A B = a 2
A. S = 4 a 15 ( a 15 + 2 a 2 )
B. S = 4 a 15 ( a 15 + a 2 )
C. S = 4 a 15 ( a 15 - 2 a 2 )
D. S = 4 a 15 ( a 15 - a 2 )
Cho hình chóp A.BCD có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A trên mặt phẳng đáy là trung điểm H của CD. Cắt hình chóp bởi mặt phẳng
α
song song với AB và CD. Tính diện tích S của thiết diện thu được, biết
d
B
;
α
a
2
v
à
A
B
a
2...
Đọc tiếp
Cho hình chóp A.BCD có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A trên mặt phẳng đáy là trung điểm H của CD. Cắt hình chóp bởi mặt phẳng α song song với AB và CD. Tính diện tích S của thiết diện thu được, biết d B ; α = a 2 v à A B = a 2
A. S = 4 a 15 a 15 + 2 a 2
B. S = 4 a 15 a 15 - a 2
C. S = 4 a 15 a 15 - 2 a 2
D. S = 4 a 15 a 15 + a 2
Cho hình chóp S.ABCD có đáy hình vuông cạnh a, SA7a và SA vuông góc với mặt phẳng đáy. Gọi G, I, J thứ tự là trọng tâm của các tam giác SAB, SAD và trung điểm của CD. Diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng (GIJ) bằng A.
3
33
a
2
8
B.
23...
Đọc tiếp
Cho hình chóp S.ABCD có đáy hình vuông cạnh a, SA=7a và SA vuông góc với mặt phẳng đáy. Gọi G, I, J thứ tự là trọng tâm của các tam giác SAB, SAD và trung điểm của CD. Diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng (GIJ) bằng
A. 3 33 a 2 8
B. 23 a 2 60
C. 31 33 a 2 45
D. 93 a 2 40
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a. Mặt phẳng qua AB và trung điểm M của SC cắt hình chóp theo thiết diện có chu vi bằng 7a (tham khảo hình vẽ bên). Thể tích của khối nón có đỉnh là S và đường tròn ngoại tiếp tứ giác ABCD bằng: A.
2
6
9
πa
3
B.
6
3
πa
3
C. ...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a. Mặt phẳng qua AB và trung điểm M của SC cắt hình chóp theo thiết diện có chu vi bằng 7a (tham khảo hình vẽ bên). Thể tích của khối nón có đỉnh là S và đường tròn ngoại tiếp tứ giác ABCD bằng:
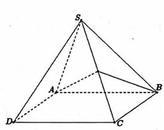
A. 2 6 9 πa 3
B. 6 3 πa 3
C. 2 3 3 πa 3
D. 2 6 3 πa 3