Các câu hỏi tương tự
Cho hình chóp tứ giác đều S.ABCD có đáy bằng a, và cạnh bên bằng a√2.a) Tính thể tích của hình chóp đã cho.b) Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.c) Gọi A’ và C lần lượt là trung điểm của hai cạnh SA và SC. Chứng minh rằng hình chóp A’.ABCD và C’.CBAD bằng nhau.giúp với
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy bằng a, và cạnh bên bằng a√2.
a) Tính thể tích của hình chóp đã cho.
b) Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
c) Gọi A’ và C' lần lượt là trung điểm của hai cạnh SA và SC. Chứng minh rằng hình chóp A’.ABCD và C’.CBAD bằng nhau.
giúp với![]()
Câu 1: Cho hình chóp tứ giác đều S.ABCD có đáy bằng a, và cạnh bên bằng a√2.
a) Tính thể tích của hình chóp đã cho.
b) Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
c) Gọi A’ và C lần lượt là trung điểm của hai cạnh SA và SC. Chứng minh rằng hình chóp A’.ABCD và C’.CBAD bằng nhau.
Câu 2: Trong không gian tọa độ Oxyz cho các điểm A(4; -1; 2); B(1; 2; 2), C(1; -1; 5)
a) Chứng minh rằng ABC là tam giác đều.
b) Viết Phương trình mp(ABC). Tính thể tích khối tứ diện giới hạn bởi mp(ABC)...
Đọc tiếp
Câu 1: Cho hình chóp tứ giác đều S.ABCD có đáy bằng a, và cạnh bên bằng a√2.
a) Tính thể tích của hình chóp đã cho.
b) Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
c) Gọi A’ và C' lần lượt là trung điểm của hai cạnh SA và SC. Chứng minh rằng hình chóp A’.ABCD và C’.CBAD bằng nhau.
Câu 2: Trong không gian tọa độ Oxyz cho các điểm A(4; -1; 2); B(1; 2; 2), C(1; -1; 5)
a) Chứng minh rằng ABC là tam giác đều.
b) Viết Phương trình mp(ABC). Tính thể tích khối tứ diện giới hạn bởi mp(ABC) và các mặt phẳng tọa độ.
c) Viết phương trình trục của đường tròn ngoại tiếp ΔABC
d) Tìm tọa độ điểm D sao cho ABCD là tứ diện đều.
các bạn giúp mình với
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Gọi M, N lần lượt là trung điểm của SB và SD. Biết AM vuông góc với CN. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD. A.
2
a
10
B.
3
a
10
C....
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Gọi M, N lần lượt là trung điểm của SB và SD. Biết AM vuông góc với CN. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
A. 2 a 10
B. 3 a 10
C. a 10
D. 4 a 10
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên bằng
a
3
. Gọi
V
1
,
V
2
lần lượt thể tích khối cầu và khối nón ngoại tiếp hình chóp S.ABCD. Tính tỷ số
V
1
V
2
A.
V
1
V...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên bằng a 3 . Gọi V 1 , V 2 lần lượt thể tích khối cầu và khối nón ngoại tiếp hình chóp S.ABCD. Tính tỷ số V 1 V 2
A. V 1 V 2 = 324 25 .
B. V 1 V 2 = 18 30 25 .
C. V 1 V 2 = 36 25 .
D. V 1 V 2 = 108 25 .
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng a
2
. Mặt phẳng (P) qua A và vuông góc với SC cắt SB, SC, SD lần lượt tại E, I, F. Tính tỉ số k giữa thể tích hình chóp S.AEIF và thể tích hình chóp S.ABCD. A.
k
1
4
B.
k
1
3
C.
k
1
6...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng a 2 . Mặt phẳng (P) qua A và vuông góc với SC cắt SB, SC, SD lần lượt tại E, I, F. Tính tỉ số k giữa thể tích hình chóp S.AEIF và thể tích hình chóp S.ABCD.
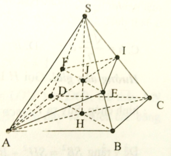
A. k = 1 4
B. k = 1 3
C. k = 1 6
D. k = 2 9
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Gọi M và N lần lượt là trung điểm của SA và CD. Cho biết MN tạo với mặt đáy một góc bằng
30
0
. Tính thể tích khối chóp S.ABCD .
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Gọi M và N lần lượt là trung điểm của SA và CD. Cho biết MN tạo với mặt đáy một góc bằng 30 0 . Tính thể tích khối chóp S.ABCD .
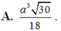
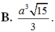
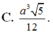
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và SA a. Gọi E là trung điểm của cạnh AB. Diện tích mặt cầu ngoại tiếp hình chóp bằng .SBCE A.
14
πa
2
B.
11
πa
2
C.
8
πa
2
D.
12
πa
2
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và SA = a. Gọi E là trung điểm của cạnh AB. Diện tích mặt cầu ngoại tiếp hình chóp bằng .SBCE
A. 14 πa 2
B. 11 πa 2
C. 8 πa 2
D. 12 πa 2
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Cạnh bên SA vuông góc với đáy (ABCD) và SA3a. Tính bán kính R của mặt cầu ngoại tiếp khối chóp S.ABCD
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Cạnh bên SA vuông góc với đáy (ABCD) và SA=3a. Tính bán kính R của mặt cầu ngoại tiếp khối chóp S.ABCD
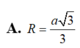
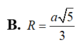
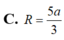
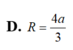
Hình chóp S.ABC là hình chóp tam giác đều, có cạnh đáy bằng a và cạnh bên bằng a 2 . Một mặt cầu đi qua đỉnh A và tiếp xúc với hai cạnh SB , SC tại trung điểm của mỗi cạnh. Gọi giao điểm thứ hai của mặt cầu với đường thẳng SA là D. Tính độ dài của AD và SD.

