Đáp án là C.
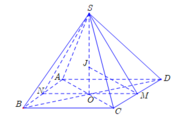
Gọi O là tâm hình vuông ABCD .Ta có đường cao của hình chóp SABCD là SO
V S A B C D = 1 3 S 0 . S A B C D ⇔ 3 6 a 8 = 1 3 S O . a 2 ⇒ S O = 3 2 a .
Xét tam giác SMO ta có SM= S 0 2 + O M 2 = ( 3 2 a ) 2 + ( a 2 ) 2 = a
Gọi M,N lần lượt là trung điểm của AB,CD.Khi đó J là tâm đường tròn nội tiếp tam giác SMN. Khi đó ta có MJ là đường phân giác của tam giác SMN.
Suy ra : S J J O = M S M O = a a = 2 ⇒ S J = 2 J O .
Mà S 0 = S J + J O = 3 2 a ⇔ 3 J O = 3 2 a ⇔ J O = 3 6

