Đáp án C.
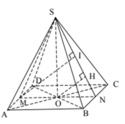
Gọi O chân đường cao hạ từ S xuống mặt đáy ⇒ A C ∩ B D = O .
Dựng O H ⊥ S N (H thuộc SN). Gọi M, N lần lượt là trung điểm của AD và BC. Trong (SMN), kẻ M I // O H (I thuộc SN).
Em có: AD//BC⇒d S B , A D = d A D , S B C = d M , S B C .
Em lại có: S M N ⊥ S B C ⇒ OH ⊥ S B C
Do O H // M I nên MI⊥SBC⇒d M , S B C = M I = 2 O H .
Tam giác SON vuông tại O, đường cao OH nên ta có
1 O H 2 = 1 S O 2 + 1 O N 2 ⇒ O H = a h 4 h 2 + a 2 ⇒ M I = 2 a h 4 h 2 + a 2