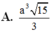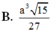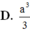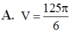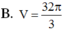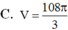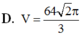Chọn A
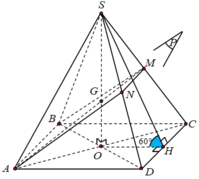
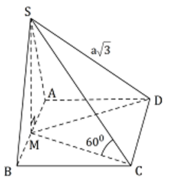
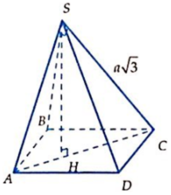
Gọi H là trung điểm cạnh CD và O là tâm hình vuông ABCD.
Ta có S. ABCD là hình chóp tứ giác đều nên các mặt bên hợp với đáy các góc bằng nhau
Giả sử S C D , A B C D ^ = S H O ^ = 60 o
Tam giác SHO vuông tại O có:
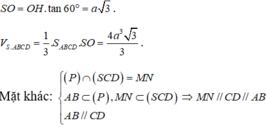
Mà G là trọng tâm tam giác SAC nên G cũng là trọng tâm tam giác SBD