Phương pháp:
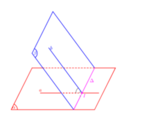

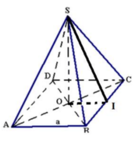
Gọi O là tâm của hình vuông ABCD. I là trung điểm của BC. Ta có:
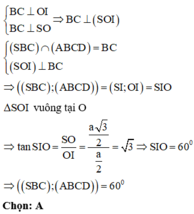
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Phương pháp:



Gọi O là tâm của hình vuông ABCD. I là trung điểm của BC. Ta có:
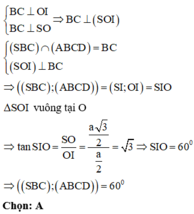
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh AB = a (a>0) Góc giữa mặt bên và mặt đáy bằng 60 ° Tính thể tích khối chóp S.ABCD:
A. a 3 3 2
B. a 3 6
C. a 3 3 3
D. a 3 3 6
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, đường cao của hình chóp bằng a 3 2 . Tính số đo góc giữa mặt bên và đáy
A. 30 o
B. 45 o
C. 60 o
D. 90 o
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, chiều cao của chóp bằng a 3 2 . Góc giữa mặt bên và mặt đáy bằng
A. 60 °
B. 75 °
C. 30 °
D. 45 °
Cho hình chóp tứ giác đều S.ABCd có cạnh đáy bằng a. Góc giữa mặt bên và mặt đáy bằng 60 ∘ . Tính thể tích V của khối chóp đã cho
A. V = a 3 6 6
B. V = a 3 3 6
C. V = a 3 3 2
D. V = a 3 3 18
Cho hình chóp tứ giác đều có cạnh đáy bằng a và độ dài đường cao bằng 14 a 2 . Tính tang của góc giữa cạnh bên và mặt đáy
A. 7
B. 14 2
C. 14
D. 7 2
Cho hình chóp tứ giác đều S.ABCD các cạnh đáy bằng a, góc giữa cạnh bên SA và mặt đáy bằng 30 o . Tính diện tích xung quanh S x q của hình trụ có một đường tròn đáy là đường tròn nội tiếp hình vuông ABCD và chiều cao bằng chiều cao của hình chóp S.ABCD
A. S x q = π a 2 6 12
B. S x q = π a 2 3 12
C. S x q = π a 2 3 6
D. S x q = π a 2 6 6
Cho hình chóp tam giác đều có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60 ° . Tính diện tích S của mặt cầu ngoại tiếp hình chóp đã cho.
A. S = 16 πa 2 9
B. S = 64 πa 2 9
C. S = 16 πa 2 3
D. S = 64 πa 2 3
Cho hình chóp đều S.ABCD có cạnh đáy bằng a góc giữa một mặt bên và mặt đáy bằng 60 ° Tính độ dài đường cao SH
A. S H = a 2 3
B. S H = a 3 2
C. S H = a 2
D. S H = a 3 3
Hình chóp tứ giác đều có cạnh đáy bằng a, chiều cao h = a 2 Góc giữa cạnh bên với mặt đáy là:
A. 60 °
B. 15 °
C. 45 °
D. 30 °