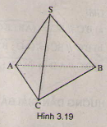
(h.3.19)
= SA.SC.cos - SA.SB.cos
= 0.
Vậy SA ⊥ BC.
\(\overrightarrow{SB}.\overrightarrow{AC}=\overrightarrow{SB}\left(\overrightarrow{SC}-\overrightarrow{SA}\right)=\overrightarrow{SB}.\overrightarrow{SC}-\overrightarrow{SB}.\overrightarrow{SA}\)
\(=SB.SC.cos\widehat{BSC}-SB.SA.cos\widehat{BSA}=0\).
Vậy \(SB\perp AC\).
\(\overrightarrow{SC}.\overrightarrow{AB}=\overrightarrow{SC}.\left(\overrightarrow{SB}-\overrightarrow{SA}\right)=\overrightarrow{SC}.\overrightarrow{SB}-\overrightarrow{SC}.\overrightarrow{SA}\)
\(=SC.SB.cos\widehat{BSC}-SC.SA.cos\widehat{CSA}=0\).
Vậy \(SC\perp AB\).


