Chọn B.
Phương pháp: Dựng đoạn vuông góc chung.
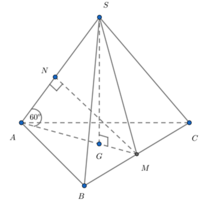
Cách giải: Gọi M là trung điểm BC, G là tâm của đáy, N là hình chiếu của M lên SA.

Chọn B.

Phương pháp: Dựng đoạn vuông góc chung.
Cách giải: Gọi M là trung điểm BC, G là tâm của đáy, N là hình chiếu của M lên SA.

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và A B = a . Cạnh bên SA vuông góc với mặt phẳng đáy , góc tạo bởi hai mặt phẳng (ABC) và (SBC) bằng 60 ° . Khoảng cách giữa hai đường thẳng AB và SC bằng
A. a
B. a 2 2
C. a 3 2
D. a 3 3
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và góc giữa đường thẳng SA với mặt phẳng (ABC) bằng 60 ° . Gọi G là trọng tâm của tam giác ABC, khoảng cách giữa hai đường thẳng GC và SA bằng
A. a 5 10
B. a 5 5
C. a 2 5
D. a 5
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , S A ⊥ A B C , góc giữa đường thẳng SB và mặt phẳng A B C bằng 60 ° . Khoảng cách giữa hai đường thẳng AC và SB bằng:
A. a 2 2
B. 2 a
C. a 15 5
D. a 7 7
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, S A ⊥ A B C , góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 60 ° . Khoảng cách giữa hai đường thẳng AC và SB bằng
A. a 2 2
B. a 15 5
C. 2a
D. a 7 7
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho HA=2HB. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60°. Tính khoảng cách d giữa hai đường thẳng SA và BC theo a.
A. d = a 42 8
B. d = a 21 12
C. d = a 42 12
D. d = a 462 66
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho H A = 2 H B . Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60°. Tính khoảng cách d giữa hai đường thẳng SA và BC theo a.
A. d = a 42 8
B. d = a 21 12
C. d = a 42 12
D. d = a 462 66
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho HA = 3HB. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60°. Tính khoảng cách giữa hai đường thẳng SA và BC theo a.
A. a 61 4
B. 4 a 17 3
C. 4 a 35 51
D. 4 a 351 3 61
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, S A ⊥ A B C , góc giữa đường thẳng SB và mặt phẳng(ABC) bằng 60 ° . Tính khoảng cách giữa hai đường thẳng AC và SB.
A. a 15 5
B. a 2 2
C. a 7 7
D. 2a
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA= 3 a và vuông góc với mặt đáy. Gọi M là trung điểm cạnh SB (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng AM và SC bằng
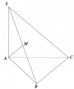
A. 5 16
B. 11 16
C. 5 8
D. 3 8