Đáp án A
Gọi H là trọng tâm tam giác ABC suy ra SH = h; SA = b
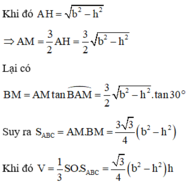
Đáp án A
Gọi H là trọng tâm tam giác ABC suy ra SH = h; SA = b
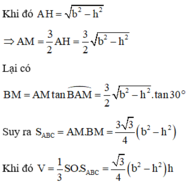
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên S C = a 15 . Tam giác SAD là tam giác đều cạnh bằng 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm AD, khoảng cách từ B đến mặt phẳng (SHC) bằng 2 a 6 . Tính thể tích V của khối chóp S.ABCD?
A. V = 8 a 3 6 .
B. V = 12 a 3 6 .
C. V = 4 a 3 6 .
D. V = 24 a 3 6 .
Cho hình chóp S.ABCDvới đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên S C = a 15 . Tam giác SAD là tam giác đều cạnh 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm của cạnh AD, khoảng cách từ B tới mặt phẳng (SHC) bằng 2 6 a . Tính thể tích V của khối chóp S,ABCD?
A. V = 8 6 a 3
B. V = 12 6 a 3
C. V = 4 6 a 3
D. V = 24 6 a 3
Cho hình chóp tam giác đều cạnh bằng 3. Tính thể tích hình chóp đó biết chiều cao h = 7.
A. 9 3 4
B. 63 3 2
C. 21 3 4
D. 63 4 3
Thể tích V của khối chóp có diện tích đáy B và chiều cao h là:
A. V=Bh
B. V=Bh/2
C. V=2Bh
D. V=Bh/3
Thể tích V của khối chóp có chiều cao bằng h và diện tích đáy bằng B là
A. V=3Bh.
B. V=Bh/3.
C. V=Bh/2.
D. V=Bh.
Công thức thể tích V của khối chóp tính theo diện tích đáy B và chiều cao h của nó là:
A. V = 2 3 B h
B. V = 1 3 B h
C. V = 1 2 B h
D. V = Bh
Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, AB = 2, các cạnh bên đều bằng 2. Tính thể tích V của khối cầu ngoại tiếp hình chóp SABC
A. V = 32 π 3
B. V = 4 3 π 27
C. V = 8 2 π 3
D. V = 8 π 3
Cho hình chóp tam giác đều có cạnh đáy bằng 1 và chiều cao h = 3 . Diện tích mặt cầu ngoại tiếp hình chóp là:
A. 100 π 3
B. 25 π 3
C. 100 π 27
D. 100 π
Cho hình chóp tam giác đều có cạnh đáy bằng 1 và chiều cao h = 3 . Diện tích mặt cầu ngoại tiếp hình chóp là:
A. 100 π 3 .
B. 25 π 3 .
C. 100 π 27 .
D. 100 π .