Question

Cho hình chóp S.ABCD, M, N, P, Q lần lượt là trọng tâm các tam giác SAB, SBC, SCD, SDA. Khẳng định nào sau đây là đúng?

A. MNPQ là hình bình hành.

B. MNPQ là hình thoi.

C. MNPQ là hình thang chỉ có một cặp cạnh đối song song.

D. MNPQ là tứ giác không có cặp cạnh nào song song.

Answer 1

Đáp án A

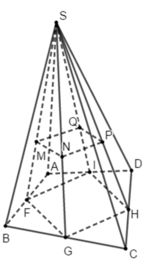
Gọi F, G, H, I lần lượt là trung điểm của AB; BC; CD và DA

Vì M, N, P, Q lần lượt là trọng tâm của các tam giác SAB, SBC, SCD, SDA.

Do đó ta có: S M S F = S N S G = S P S H = S Q S I = 2 3

Khi đó: MN // FG; NP // GH; QP // IH; MQ // FI

Xét tam giác ABD có FI là đường trung bình (vì F và I lần lượt là trung điểm của AB và AD)

Suy ra FI // BD

Chứng minh tương tự ta có: GH // BD

Nên FI // GH // BD

Tương tự FG // IH // AC

Do đó MQ // NP // FI // GH và MN // PQ // FG // IH

Vậy tứ giác MNPQ là hình bình hành.

Chọn đáp án A