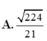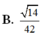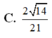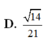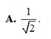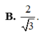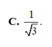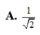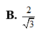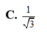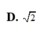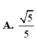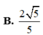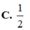Chọn A.
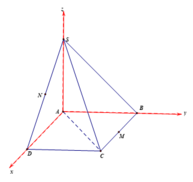
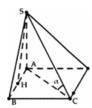
Gắn hệ trục tọa độ như hình vẽ. Khi đó ta có:
A(0;0;0), B(0;a;0), C(a;a;0), D(a;0;0), S(0;0;a)
M là trung điểm của BC ⇒ M a 2 ; a ; 0
N là trung điểm của SD ⇒ N a 2 ; 0 ; a 2 ⇒ M N → 0 ; - a ; a 2
Do ABCD là hình vuông nên AC ⊥ BD
S A ⊥ ( A B C D ) B D ⊂ ( A B C D ) ⇒ S A ⊥ B D
Ta có:
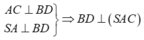
![]()
là một pháp tuyến của (SAC)
Khi đó ta có:
sin α = cos ( M N → , B D → ) = M N → . B D → M N → . B D →
= a 2 a 5 2 . a 2 = 10 5
1 sin 2 α = 1 + c o t 2 α ⇔ 25 10 = 1 + c o t 2 α ⇔ c o t 2 α = 3 2 ⇒ c o t α = 3 2 ( d o 0 < α < 90 0 )
Lại có:
tan α . c o t α = 1 ⇒ tan α = 2 3 = 6 3