Đáp án C
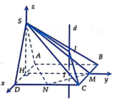
Gọi H là trung điểm của A D ⇒ S H ⊥ ( A B C D ) ⇒ S H = a 3
Cho hệ trục tọa độ như hình vẽ ⇒ D ( a ; 0 ; 0 ) , M ( 0 ; 2 a ; 0 ) , N ( a ; a ; 0 )
⇒ Trung điểm MN là I a 2 ; 3 a 2 ; 0 có S 0 ; 0 ; a 3 , C a ; 2 a ; 0
Gọi d là đường thẳng đi qua I và vuông góc với (ABCD)
⇒ d có vecto chỉ phương k → = 0 ; 0 ; 1
∆ N C M vuông tại C là tâm đường tròn ngoại tiếp
⇒ d là trục của đường tròn ngoại tiếp tam giác CMN
⇒ Tâm J của mặt cầu ngoại tiếp SCMN thuộc d
Ta có d qua I a 2 ; 3 a 2 ; 0 và k → = 0 ; 0 ; 1 là vecto chỉ phương ⇒ d : x = a 2 y = 3 a 2 z = t
⇒ J a 2 ; 3 a 2 ; t mà J C = J S ⇒ a 2 2 + a 2 2 + t 2 = a 2 2 + 3 a 2 2 + a 3 - t 2
⇒ t = 5 a 3 6 Bán kính R = J C = 93 6 a .

