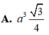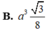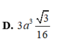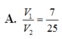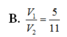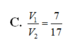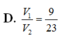Question

Cho hình chóp S.ABCD, đáy ABCD là hình bình hành, mặt phẳng  α  đi qua AB cắt cạnh SC, SD lần lượt tại M, N. Tính tỉ số  S N S D  để  α  chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.

A.  1 2

B.  1 3

C.  5 - 1 2

D.  3 - 1 2

Answer 1

Chọn C

Ta có:  α ∩ ( S C D ) = M N   ⇒ M N / / C D .

Do đó  α  là (ABMN).

Mặt phẳng  α  chia khối chóp thành 2 phần có thể tích bằng nhau là

V S . A B M N = V A B C D M N ⇒ V S . A B M N = 1 2 . V S . A B C D               1  

Ta có:

V S . A B C = V S . A C D = 1 2 V S . A B C D

 

Đặt  S N S D = x với (0<x<1), khi đó theo Ta-let ta có  S N S D = S M S C = x .

Mặt khác 

V S . A B M V S . A B C = S A S A . S B S B . S M S C = x   ⇒ V S . A B M = x 2 V S . A B C D

V S . A M N V S . A C D = S A S A . S M S C . S N S D = x 2   ⇒ V S . A M N = x 2 2 V S . A B C D

⇒ V S . A B M N = V S . A B M + V S . A M N = ( x 2 + x 2 2 ) . V S . A B C D   2

Từ (1), (2) suy ra

x 2 + x 2 2 = 1 2 ⇔ x 2 + x - 1 = 0

x = - 1 - 5 2   v à   x = - 1 + 5 2

Đối chiếu điều kiện của x ta được  S N S D = - 1 + 5 2