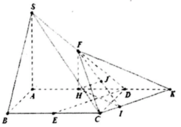
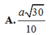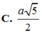Kẻ CI // BD
=> d(SC;BD) = d(BD;SCI) = d(D;SCI)
Ta có \(\dfrac{\left(D;\left(SCI\right)\right)}{\left(A;\left(SCI\right)\right)}=\dfrac{1}{2}\Rightarrow d\left(D;\left(SCI\right)\right)=\dfrac{1}{2}\left(A;\left(SCI\right)\right)=\dfrac{1}{2}AC\)
Theo Pytago tam giác ABC vuông tại A ta có
AC = \(\sqrt{AB^2+BC^2}=\sqrt{2}a\)
\(\Rightarrow\dfrac{a\sqrt{30}}{n}=\dfrac{1}{2}\sqrt{2}a\Rightarrow n=2\sqrt{15}\)
mình sửa bài nhé
Kẻ CI // BD
=> d(SC;BD) = d(BD;SCI) = d(D;SCI)
Ta có \(\dfrac{\left(D;\left(SCI\right)\right)}{\left(A;\left(SCI\right)\right)}=\dfrac{1}{2}\Rightarrow d\left(D;\left(SCI\right)\right)=\dfrac{1}{2}\left(A;\left(SCI\right)\right)\)
Dựng AH vuông SC
=> AH là kc từ (A;(SCI))
Theo Pytago tam giác ABC vuông tại A ta có
AC = \(\sqrt{AB^2+BC^2}=\sqrt{2}a\)
Xét tam giác SAB vuông tại A ta có
\(tanSBA=\dfrac{SA}{AB}\Rightarrow SA=a\sqrt{3}\)
Xét tam giác SAC vuông tại A, đường cao AH
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AC^2}\Rightarrow AH=\dfrac{\sqrt{30}}{5}a\)
\(\Rightarrow\dfrac{a\sqrt{30}}{n}=\dfrac{a\sqrt{30}}{5}\) => n = 5