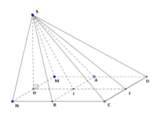
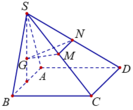
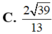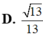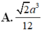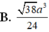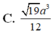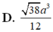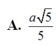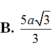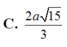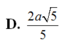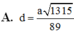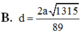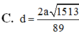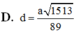Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều, SC = SD = a 3 . Tính cosin của góc giữa hai mặt phẳng (SAD) và (SBC). Gọi I là trung điểm của AB; J là trung điểm của CD. Gọi H là hình chiếu của S trên (ABCD) . Qua H kẻ đường thẳng song song với AB, đường thẳng này cắt DA và CB kéo dài tại M, N . Các nhận định sau đây.
(1) Tam giác SIJ là tam giác có S I J ^ tù.
(2) sin S I H ^ = 6 3
(3) M S N ^ là góc giữa hai mặt phẳng (SBC) và (SAD).
(4) cos M S N ^ = 1 3
Chọn đáp án đúng:
A. (1), (2) đúng , (3) sai
B. (1), (2), (3) đúng (4) sai
C. (3), (4) đúng (1) sai
D. (1), (2), (3), (4) đúng