Đáp án B
Gọi H 1 là chân đường cao kẻ từ H đến DC. H 2 là chân đường cao kẻ từ H đến S H 1 . Khi đó ta có
![]()
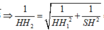
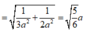
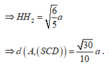
=> Chọn phương án B.
Đáp án B
Gọi H 1 là chân đường cao kẻ từ H đến DC. H 2 là chân đường cao kẻ từ H đến S H 1 . Khi đó ta có
![]()
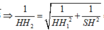
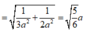
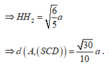
=> Chọn phương án B.
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB 2a; BC = \(\dfrac{3a}{2}\); AD = 3a. Hình chiếu vuông góc của S lên (ABCD) l;à trung điểm H của BD. Biết góc giữa (SCD) và (ABCD) bằng 60 độ. Tình khoảng cách từ C đến (SBD)?
Cho hình chóp S.ABCD, đáy là hình thang vuông tại A và B, biết AB=BC=a, AD=2a, SA= a 3 và SA ⊥ (ABCD) Gọi M và N lần lượt là trung điểm của SB, SA. Tính khoảng cách từ M đến (NCD) theo a
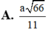
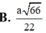
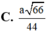
![]()
Bài 4. Cho hình chóp S.ABC , hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của AC, đáy ABC là tam giác vuông ở B, SA = 2a, AB = av3, BC = a. Tính góc (SH,(SAB)). Bài 5. Cho hình chóp S.ABCD, SA1(ABCD), đáy ABCD là hình vuông cạnh a, góc giữa mặt phăng (SBC) và (ABCD) bằng 30°. Tính góc (AD.(SCD)).
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = BC = a, AD = 2a. Cạnh bên SA vuông góc với đáy và SC tạo với (SAD) góc 30 o . Gọi G là trọng tâm tam giác SAB. Tính khoảng cách từ G đến mặt phẳng (SCD).
Cho hình chóp S.ABCD có SA \(\perp\)(ABCD) và ABCD là hình thang vuông tại A, đáy lớn AB, AB=2a, AD=CD=a. Gọi H là hình chiếu vuông góc của A lên SC và E là trung điểm của AB
a, CMR: (SCD)\(\perp\)(SAD) và AH \(\perp\)(SBC)
b, Biết góc giữa 2 mp (SCD) và (ABCD) bằng 300. Tính góc giữa 2 mp (SAD) và (SCE)?
Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật,AB=a, AD=2a. Đường cao SA bằng 2a. Khoảng cách từ trung điểm M của SB đến mặt phẳng (SCD) bằng
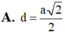
![]()
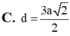
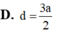
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB=BC=a ,AD=2a Cạnh SA=2a và SA vuông góc với mặt phẳng (ABCD). Gọi M là trung điểm của cạnh AB và ( α ) là mặt phẳng qua M và vuông góc với AB. Diện tích thiết diện của mặt phẳng ( α ) với hình chóp S.ABCD là
![]()


![]()
: Cho hình chóp S.ABCD có SA⊥(ABCD) và SA=a; đáy ABCD là hình thang vuông có đáy bé là BC, biết AB=BC=a, AD=2a.
1) Chứng minh các mặt bên của hình chóp là các tam giác vuông
2) Tính khoảng cách giữa AB và SD
3) M, H là trung điểm của AD, SM cm AH⊥(SCM)
4) Tính góc giữa SD và (ABCD); SC và (ABCD)
5) Tính góc giữa SC và (SAD)
6) Tính tổng diện tích các mặt của chóp.
Cho hình chóp SABCD là hình thang vuông tại A và B. AD=2a, SA=a căn 3, AB=BC=a. SA vuông góc với đáy. Tính khoảng cách từ. a)A đến (SBC) b)A đến (SCD) c)BC đến (SAD)