Đáp án A
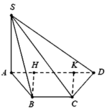
Gọi H, K lần lượt là hình chiếu của B, C trên AD
Gọi α là góc giữa 2 mặt phẳng S A D , S B C
⇒ Δ S H K là hình chiếu của Δ S B C trên S A D ⇒ c o s α = S S H K S S B C
Ta có H K = B C = 2 a ⇒ S S H K = 1 2 S A . H K = a 3 .2 a 2 = a 2 3
Lại có d A ; B C = B H = a 3 ⇒ d S ; B C = a 3 . 2 = a 6
Suy ra S S B C = 1 2 d S ; B C . B C = a 3 6 .
Vậy c o s α = a 3 3 a 3 6 = 2 2

