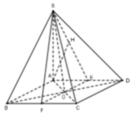
Gọi E, F lần lượt là trung điểm của AD, BC thì AB / / EF ⇒ AB / / (SEF)
Mà ![]()
![]()
Dựng A H ⊥ S E
Ta thấy: FE / / AB, A B ⊥ ( S A D ) ⇒ F E ⊥ ( S A D ) ⇒ F E ⊥ A H
Mà A H ⊥ S E nên A H ⊥ ( S E F ) ⇔ d ( A , ( S E F ) ) = A H
ABCD là hình vuông cạnh a nên B D = a 2
Dễ dàng chứng minh được ∆ S A B = ∆ S A D c . g . c ⇒ S B = S D
Tam giác SBD cân có S B D = 60 ° nên đều ⇒ S D = B D = a 2
Tam giác SAD vuông tại A có S A = S D 2 - A D 2 = 2 a 2 - a 2 = a
Tam giác SAE vuông tại A có


Do đó
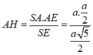
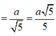
Chọn đáp án D.

