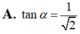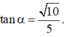Đáp án A
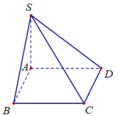
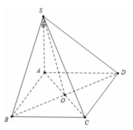
Gọi N là trung điểm AD suy ra HN // BD.
Góc giữa BD và (SAD) bằng góc giữa HN và (SAD).
Ta có AD⊥SH, AD⊥AB suy ra AD⊥ (SAB) . Trong mặt phẳng (SAB) kẻ HK⊥SA nên ta suy ra AD⊥HK và HK⊥ (SAD) . vậy góc giữa HN và (SAD) là góc HNK.
Gọi cạnh của hình vuông là a
Ta tính được HN = a 2 2 . Xét tam giác vuông SHA vuông tại H ta có
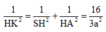
![]()
Xét tam giác vuông HNK vuông tại K ta có ![]()