Đáp án B
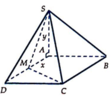
S A = y = a 2 - x 2 ; S A B C M = B C + A M 2 . A B = a + x 2 . a
S A B C M = 1 3 S A B C M . S A = a 6 ( a + x ) a 2 - x 2
Xét hàm số f ( x ) = ( a + x ) a 2 - x 2 trên 0 ; a ta được:
m a x 0 ; a f ( x ) = f a 2 = 3 3 a 2 4 ⇒ V m a x = a 3 3 8

