Đáp án A
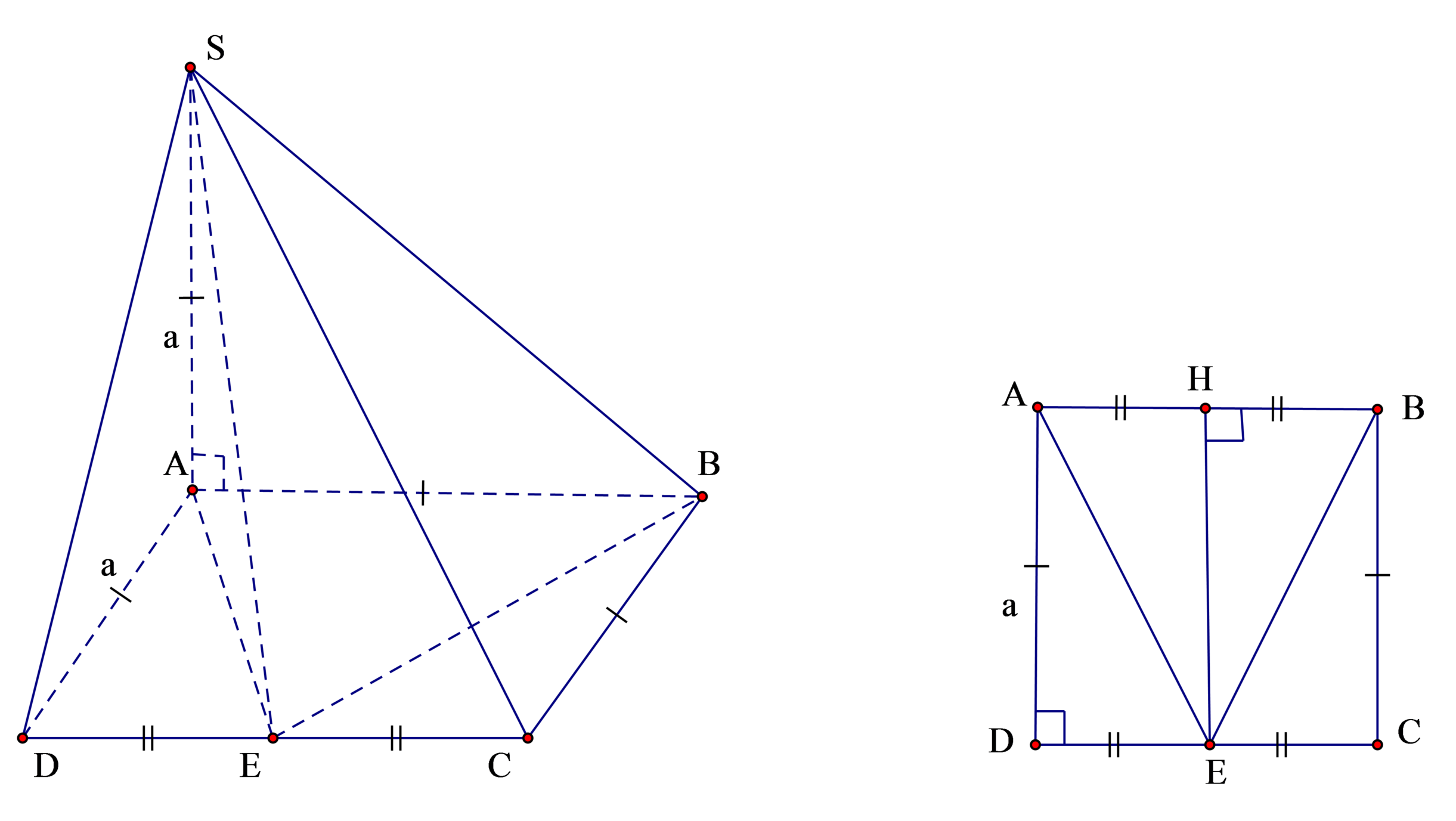
Hình chóp SABE có cạnh bên S A ⊥ đáy (ABE) ta có công thức tính bán kính mặt cầu của hình chóp dạng này là R = R d 2 + h 2 2 ( với R d là bán kính đường tròn ngoại tiếp đáy và h là chiều cao hình chóp )
Ta có: h = S A = a ; d t A B E = 1 2 E H . A B = a 2 2
A E = B E = a 2 + a 2 4 = a 5 2
R d = A B . A E . B E 4 d t A B E = a . 5 a 2 4 4. a 2 2 = a 5 8
vậy R = 25 a 64 2 + a 2 4 = a 41 8 .

