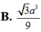Đáp án A
Gọi H là trung điểm của AB .
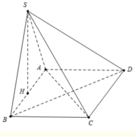
Lại có: S A B ⊥ A B C D ⇒ S H ⊥ A B C D .
Do A D / / B C nên giao tuyến d của (SAD) và (SBC) đi qua S và song song với AD.
Do A D ⊥ A B A D ⊥ S H ⇒ A D ⊥ S A B ⇒ d ⊥ S A B .Suy ra góc giữa hai mặt phẳng (SAD) và (SBC) bằng 180 ∘ − AS B ⏜ = 60 ∘ .