Đáp án C
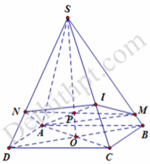
Bài toán sử dụng bổ đề sau: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng (P) bất kì cắt các cạnh SA, SB, SC, SD lần lượt tại các điểm A’, B’, C’, D’ với tỉ số
S A ' S A = x ; S B ' S B = y ; S C ' S C = z ; S D ' S D = t thì ta có đẳng thức
1 x + 1 z = 1 y + 1 t và tỉ số
V S . A ' B ' C ' D ' V S . A B C D = x y z t 4 1 x + 1 y + 1 z + 1 t
Áp dụng vào bài toán
đặt u = S M S B , v = S N S D ta có
1 u + 1 v = S A S A ' + S C S I = 1 1 + 1 2 3 = 5 2 ≥ 2 u v ≥ 16 25 ⇒ V ' V = u v .1. 2 3 4 1 u + 1 v + 1 1 + 1 2 3 = 5 u v 6 ≥ 8 15

