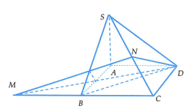
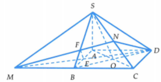
Cho hình chóp S.ABCD có A B C ⏜ = A D C ⏜ = 90 ∘ , cạnh bên SA vuông góc với mặt phẳng (ABCD), góc tạo bởi SC và mặt phẳng đáy bằng 60 ∘ , C D = a và tam giác ADC có diện tích bằng a 2 3 2 . Diện tích mặt cầu S m c ngoại tiếp hình chóp S.ABCD là
A. S m c = 16 π a 2
B. S m c = 4 π a 2
C. S m c = 32 π a 2
D. S m c = 8 π a 2
Đáp án A
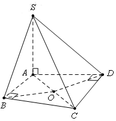
Tam giác ADC vuông tại D ⇒ S Δ A D C = 1 2 . A D . C D = a 2 3 2
⇒ C D = a 3 ⇒ A C = A D 2 + C D 2 = a 2 + a 3 2 = 2 a .
Vì tứ giác ABCD có A B C ⏜ = A D C ⏜ = 90 ∘ ⇒ A B C D là tứ giác nội tiếp đường tròn tâm O với O là trung điểm của AC ⇒ R A B C D = A C 2 = a .
Và S A ⊥ A B C D ⇒ S C ; A B C D ⏜ = S C ; A C ⏜ = S C A ⏜ = 60 ∘
Tam giác SAC vuông tại A ⇒ tan S C A ⏜ = S A A C ⇒ S A = 2 a 3 .
Suy ra bán kính mặt cầu cần tính là:
R = R 2 A B C D + S A 2 4 = 2 a ⇒ S m c = 16 π a 2 .