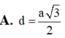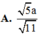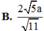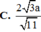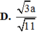Question

Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA vuông góc (ABC), SB=2a. G là trọng tâm tam giác ABC. Tính khoảng cách từ G đến (SBC).

Answer 1

Gọi H là trung điểm BC

Ta có: \(d\left(G,\left(SBC\right)\right)=\dfrac{1}{3}d\left(A,\left(SBC\right)\right)\) (vì \(GH=\dfrac{1}{3}AH\))

Vì \(\left\{{}\begin{matrix}AH\perp BC\\SA\perp BC\end{matrix}\right.\Rightarrow BC\perp\left(SAH\right)\)

Vẽ \(AK\perp SH\Rightarrow BC\perp AK\left(BC\perp\left(SAH\right)\right)\Rightarrow AK\perp\left(SBC\right)\)

\(\Rightarrow d\left(A,\left(SBC\right)\right)=AK\)

Ta có: \(SB^2=SA^2+AB^2\Rightarrow4a^2=SA^2+a^2\Rightarrow SA^2=3a^2\)

\(AH^2=AB^2-BH^2=a^2-\dfrac{1}{4}a^2=\dfrac{3}{4}a^2\)

\(\Rightarrow\dfrac{1}{AK^2}=\dfrac{1}{SA^2}+\dfrac{1}{AH^2}=\dfrac{1}{3a^2}+\dfrac{1}{\dfrac{3}{4}a^2}\Rightarrow AK=\dfrac{\sqrt{15}}{5}a\)

\(\Rightarrow d\left(G,\left(SBC\right)\right)=\dfrac{1}{3}.AK=\dfrac{\sqrt{15}}{15}a\)