Đáp án B
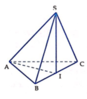
Gọi I là hình chiếu của điểm S trên mặt phẳng (ABC). Do S A = S B = S C nên I A = I B = I C ⇒ I là tâm đường tròn ngoại tiếp Δ A B C . Mà Δ A B C vuông cân tại A nên I là trung điểm của BC và I A = I B = I C = 1 2 B C = a 2 2 .
Ta có IA là hình chiếu của SA trên mặt phẳng (ABC) nên S A , A B C ^ = S A , I A ^ = S A I ^ = 45 0 .
Do Δ S I A vuông tại I nên Δ S A I vuông cân tại I, khi đó : S I = I A = a 2 2 ⇒ d S ; A B C = S I = a 2 2

