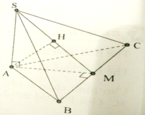
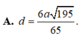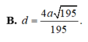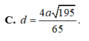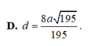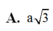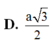Kẻ AH vuông BC với H là trung điểm
Ta có AH vuông BC
SA vuông BC
=> BC vuông (SAH)
Dựng AK vuông SH tại K
Do BC vuông (SAH) => BC vuông AK
mà SH giao BC tại H; SH;BC chứa (SBC)
=> AK vuông (SBC)
Xét tam giác SAH vuông tại A ADHT
\(\dfrac{1}{AK^2}=\dfrac{1}{SA^2}+\dfrac{1}{AH^2}\)
Ta có AH = \(\dfrac{a\sqrt{3}}{2};SA=h\)
\(\Rightarrow\dfrac{1}{AK^2}=\dfrac{1}{h^2}+\dfrac{1}{\dfrac{3a^2}{4}}=\dfrac{\dfrac{3a^2}{4}+h^2}{\dfrac{3a^2h^2}{4}}\)
\(\Rightarrow AK^2=\dfrac{\dfrac{3a^2h^2}{4}}{\dfrac{3}{4}a^2+h^2}\Rightarrow AK=\dfrac{\sqrt{3}ah}{\sqrt{3a^2+4h^2}}\)