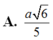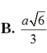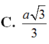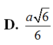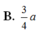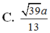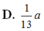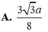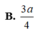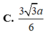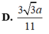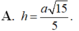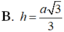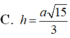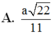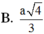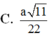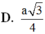Chọn D
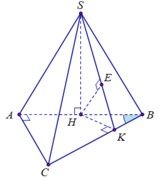
Ta có tam giác ABC vuông tại A góc A B C ^ = 30 o và BC = a, suy ra AC = a 2 , AB = a 3 2
Lại có S A B ⊥ A B C C A ⊥ A B ⇒ A C ⊥ S A B , suy ra tam giác SAC vuông tại A.
Suy ra S A = S C 2 - A C 2 = a 2 - a 2 2 = a 3 2
Tam giác SAB có S A = a 3 2 , A B = a 3 2 , S B = a SB=a. Từ đó sử dụng công thức Hê-rông ta tính được S S A B = a 2 2 4 ⇒ S H = 2 S S A B A B = a 6 3 ⇒ B H = a 3 3 = 2 A B 3 .
Suy ra d(H,(SBC)) = 2 3 d A , S B C . Từ H kẻ H K ⊥ B C .
Kẻ H E ⊥ S K ⇒ H E ⊥ S B C
Ta dễ tính được H K = a 3 6 ⇒ d H , S B C = a 6 9 .
Vậy d A , S B C = 3 2 d H , S B C = 3 2 . a 6 9 = a 6 6 .