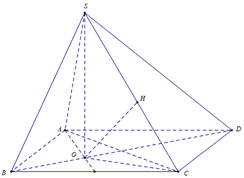
Từ giả thiết suy ra: hình chóp S.ABC là hình chóp đều.
Gọi G là trọng tâm tam giác A B C ⇒ S G ⊥ A B C D
A B / / C D ⇒ A B / / S C D ⇒ d A B ; S C = d A B ; S C D = d B ; S C D = 3 2 d G ; S C D
(Vì B D G D = 3 2 ).
Trong mp (ABCD) vẽ G C ⊥ C D , C D ⊥ S G ⇒ C D ⊥ S G C ⇒ S G C ⊥ S C D
Mà S G C ∩ S C D = S C , vẽ G H ⊥ S C ⇒ d G ; S C D = G H
G B = G C = 2 3 . a 3 2 = a 3 3 .
⇒ S G = S B 2 − B G 2 = 4 a 2 − a 2 3 = a 11 3
Tam giác SHG vuông tại G:
1 G H 2 = 1 S G 2 + 1 G C 2 = 3 11 a 2 + 3 a 2 = 36 11 a 2 ⇒ G H = a 11 6
Vậy d A B ; S C = a 11 4

