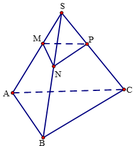
Cho hình chóp S . A B C có M là điểm di động trên cạnh SA sao cho S M S A = k . Gọi (α) là mặt phẳng đi qua M và song song với mặt phẳng A B C . Tìm k để mặt phẳng (α) cắt hình chóp S . A B C theo một thiết diện có diện tích bằng một nửa diện tích tam giác ABC.
A. k = 2 2 .
B. k = 1 2 .
C. k = 3 2 .
D. k = 1 3 .
Đáp án A
Gọi N, P là hai điểm lần lượt thuộc S B , S C thỏa mãn M N / / A B , M P / / A C .
Ta có M N // A B ⇒ M N // A B C M P // A C ⇒ M P // A B C ⇒ M N P / / A B C .
Gọi h 1 là đường cao của ΔMNP ứng với đáy MN.
Gọi h 2 là đường cao của ΔABC ứng với đáy AB.
Dễ thầy ΔMNP đồng dạng ΔABC ta có M N A B = h 1 h 2 = k .
Vậy để thỏa mãn yêu cầu bài toán
S Δ M N P S Δ A B C = 1 2 h 1 . M N 1 2 h 2 . A B = 1 2 ⇔ k . k = 1 2 ⇔ k = 2 2