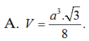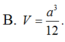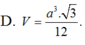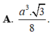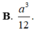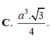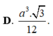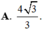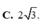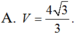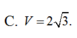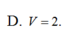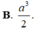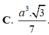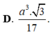hình như đáp số hơi xấu thì phải bạn ạ? :D có gì check lại các phép toán hộ mình nhé
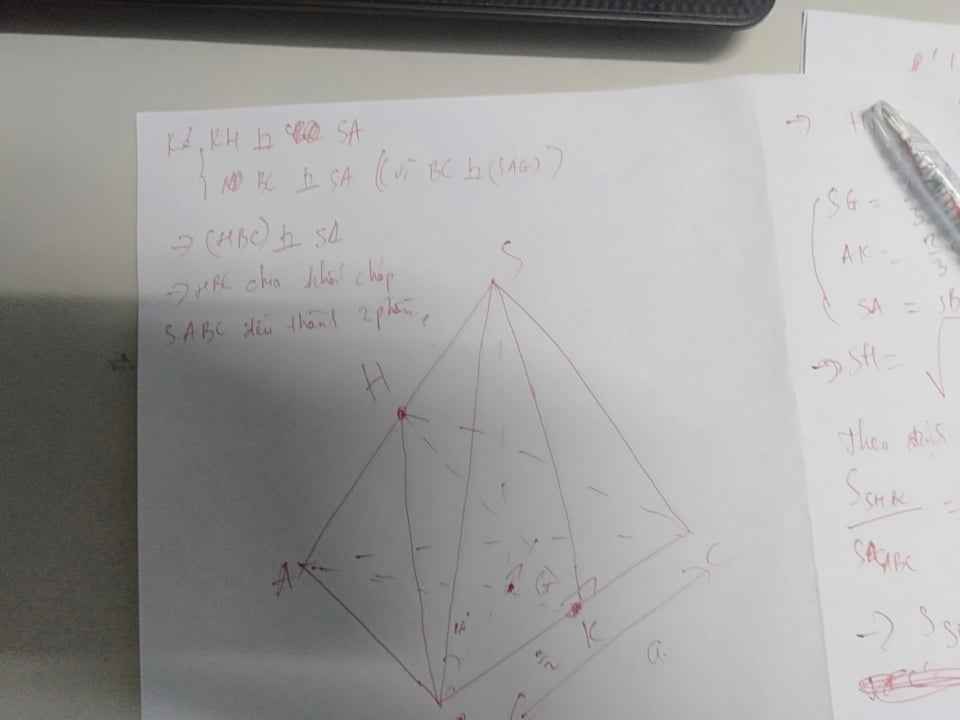
Hình vẽ minh họa và các thao tác vẽ hình ở bên dưới
Dễ tính: \(SK=\sqrt{SB^2-BK^2}=\dfrac{a\sqrt{7}}{6}\)
Ta lại có: \(S_{SAK}=\dfrac{1}{2}SG.AK=\dfrac{1}{2}HK.SA\)
\(\Rightarrow HK=\dfrac{SG.AK}{SA}=\dfrac{a}{3}\) Trong đó: \(SG=\dfrac{a}{3};AK=\dfrac{2a}{3};SA=SB=SC=\dfrac{2a}{3}\) ( Tam giác SAK cân tại A )
\(\Rightarrow SH=\sqrt{SK^2-HK^2}=\dfrac{a\sqrt{3}}{6}\)
Theo định lý Symson: \(\dfrac{S_{SHBC}}{S_{SABC}}=\dfrac{SH}{SA}=\dfrac{\sqrt{3}}{4}\Rightarrow S_{SHBC}=\dfrac{\sqrt{3}}{4}S_{SABC}\) (1)
\(\Rightarrow S_{HABC}=\left(\dfrac{4-\sqrt{3}}{4}\right)S_{SABC}\) (2)
Từ (1) và (2) suy ra được tỉ lệ thể tích giữa 2 phần là: \(\dfrac{3+4\sqrt{3}}{13}\)