Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Cho hình bs.30 (hình bình hành MNPQ có diện tích S và X, Y tương ứng là trung điểm của các cạnh QP, PN). Khi đó, diện tích của tứ giác MXPY bằng:
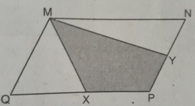
(A) 1/4 S;
(B) 1/2 S;
(C) 1/8 S;
(D) 3/4 S.
Cho hình bs.31, (R là điểm bất kì trên QS, S là điểm bất kì trên NO, hình thang NOPQ có diện tích S). Khi đó, tổng diện tích của hai tam giác QSP và NRO bằng:
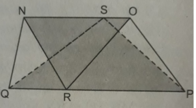
(A) 1/2 S; (B) 1/4 S;
(C) 3/4 S; (D) S
Cho hình bs.29, trong đó HK = KF = FL = LT và tam giác GHT có diện tích S. Khi đó, diện tích của tam giác GKL bằng:
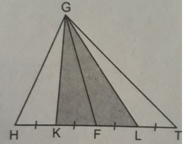
(A) 1/2 S;
(B) 1/4 S;
(C) 1/8 S;
(D) 3/4 S.
cho hình chóp S.ABC, biết tam giác sab vuông tại đỉnh S và có AB= 3 cm, SA=1cm. Tam giác sbc vuông tại đỉnh S vf có AC =4cm
1 chứng minh AS vuông góc với mặt phẳng SBC
2 tính diện tích xung quanh của hình chóp
3 tính thể tích của hình chóp
cho hình thang ABCD có đáy lớn là CD . gọi O là giao điểm của 2 đường chéo AC và BD . các đường kẻ từ A và B lần lượt song song với BC và AD , cắt đường chéo BD và AC tương ứng ở E và Fa) chứng minh AB // EFb) gọi S1, S2, S3, S4 lần lượt là diện tích các tam giác OAB, OCD, OAD, OBC và S1, S2, S3, S4, là các số nguyên. chứng minh S1.S2.S3.S4 là số chính phương
Đọc tiếp
cho hình thang ABCD có đáy lớn là CD . gọi O là giao điểm của 2 đường chéo AC và BD . các đường kẻ từ A và B lần lượt song song với BC và AD , cắt đường chéo BD và AC tương ứng ở E và F
a) chứng minh AB // EF
b) gọi S1, S2, S3, S4 lần lượt là diện tích các tam giác OAB, OCD, OAD, OBC và S1, S2, S3, S4, là các số nguyên. chứng minh S1.S2.S3.S4 là số chính phương
Bài 1: Cho tam giác MNP có MI là đường trung tuyến của tam giác. Trên MP lấy theo thứ tự MKKHHP, NK cắt MI tại O. 1) Tứ giác OKHI là hình gì?2) Chứng minh NO 30K3) So sánh : SMNI và SMIPBài 2: Cho hình thang MNPQ (MN//PQ) các đường phân giác của các góc ngoài đỉnh M và Q cắt nhau tại I. Các đường phân giác của các góc ngoài đỉnh N và P cắt nhau tại K. Chứng minh rằng: 1) MI vuông góc TQ và NK vuông góc PK2) IK//PQ
Đọc tiếp
Bài 1: Cho tam giác MNP có MI là đường trung tuyến của tam giác. Trên MP lấy theo thứ tự MK=KH=HP, NK cắt MI tại O.
1) Tứ giác OKHI là hình gì?
2) Chứng minh NO =30K
3) So sánh : SMNI và SMIP
Bài 2: Cho hình thang MNPQ (MN//PQ) các đường phân giác của các góc ngoài đỉnh M và Q cắt nhau tại I. Các đường phân giác của các góc ngoài đỉnh N và P cắt nhau tại K. Chứng minh rằng:
1) MI vuông góc TQ và NK vuông góc PK
2) IK//PQ
Gọi O là giao điểm của hai đường chéo AC, BD của hình thang ABCD với đáy lớn là CD. Các đường thẳng kẻ từ A, B song song với AC, BD cắt các đường chéo AC, BD tại E, F.a) Chứng minh tứ giác ABFE là hình thang.b) Chứng minh AB2ÈF.CDc) S1,S2,S3,S4 là diện tich các tam giác OAB, OCD, OAD VÀ OBC. Chứng minh S1.S2S3.S4d) đường thẳng qua O song song với AB cắt AD, BC tại M,N. Chứng minh 1/AB+1/CD2/MN
Đọc tiếp
Gọi O là giao điểm của hai đường chéo AC, BD của hình thang ABCD với đáy lớn là CD. Các đường thẳng kẻ từ A, B song song với AC, BD cắt các đường chéo AC, BD tại E, F.
a) Chứng minh tứ giác ABFE là hình thang.
b) Chứng minh AB2=ÈF.CD
c) S1,S2,S3,S4 là diện tich các tam giác OAB, OCD, OAD VÀ OBC. Chứng minh S1.S2=S3.S4
d) đường thẳng qua O song song với AB cắt AD, BC tại M,N. Chứng minh 1/AB+1/CD=2/MN
Cho tam giác ABC(AB<BC) vuông tại B. Đường cao BH . Vẽ HE vuông góc AB tại E , HF vuông góc BC tại F . EF giao với BH tại I
1. CM: BH= EF
2. Gọi M,N lần lượt là trung điểm của AH và CH. CM: NI là phân giác của góc HNF
3. CM .a. Tứ giác EFNM là hình thang vuông
b. S tam giác ABC =2 S EFNM
4. Tìm điều kiện của tam giác ABC để hình thang EFNM là hình chữ nhật
Cho hình thang ABCD đấy lớn CD gọi O là giao điểm 2 đường chéo AC và BD. Các đường thẳng kẻ từ A và B lần lượt song song với BC và AD cắt các đường chéo BD và AC tương ứng tại F, Ea, Chứng tỏ EF song song với ABb, Chứng tỏ AB2 EF . CDc, Gọi S1, S2, S3, S4 lần lượt là diện tích của Delta OAB,Delta OCD,Delta OAD,Delta OBCchứng tỏ S1.S2S3.S4
Đọc tiếp
Cho hình thang ABCD đấy lớn CD gọi O là giao điểm 2 đường chéo AC và BD. Các đường thẳng kẻ từ A và B lần lượt song song với BC và AD cắt các đường chéo BD và AC tương ứng tại F, E
a, Chứng tỏ EF song song với AB
b, Chứng tỏ AB2 = EF . CD
c, Gọi S1, S2, S3, S4 lần lượt là diện tích của \(\Delta OAB,\Delta OCD,\Delta OAD,\Delta OBC\)
chứng tỏ S1.S2=S3.S4