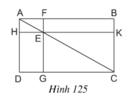
Ta có: SEHDG = SADC – SAHE – SEGC.
SEFBK = SABC – SAFE – SEKC.
Để chứng minh SEHDG = SEFBK,
ta đi chứng minh SADC = SABC; SAHE = SAFE ; SEGC = SEKC.
+ Chứng minh SADC = SABC.
SADC = AD.DC/2;
SABC = AB.BC/2.
ABCD là hình chữ nhật ⇒ AB = CD, AD = BC
⇒ SADC = SABC.
+ Chứng minh SAHE = SAFE (1)
Ta có: EH // AF và EF // AH
⇒ AHEF là hình bình hành
Mà Â = 90º
⇒ AHEF là hình chữ nhật
⇒ SAHE = SAFE (2)
+ Chứng minh SEGC = SEKC
EK // GC, EG // KC
⇒ EGCK là hình bình hành
Mà D̂ = 90º
⇒ EGCK là hình chữ nhật
⇒ SEGC = SEKC (3).
Từ (1); (2); (3) suy ra đpcm.