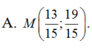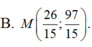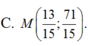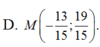Dễ thấy A, B nằm cùng phía so với đường thẳng \(\Delta\)
Gọi B' đối xứng với B qua \(\Delta\)
Đường thẳng BB' đi qua B và vuông góc với \(\Delta\) có phương trình:
\(x+y-10=0\)
Giao điểm H của BB' và \(\Delta\) có tọa độ là nghiệm hệ
\(\left\{{}\begin{matrix}x+y-10=0\\x-y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{9}{2}\\y=\dfrac{11}{2}\end{matrix}\right.\Rightarrow H=\left(\dfrac{9}{2};\dfrac{11}{2}\right)\)
\(\Rightarrow B'=\left(3;7\right)\)
Phương trình đường thẳng AB' là:
\(4x-y-5=0\)
Khi đó \(MA+MB=MA+MB'\ge AB'=2\sqrt{17}\)
\(min=2\sqrt{17}\Leftrightarrow M=\Delta\cap AB'\)
\(\Rightarrow M\) có tọa độ là nghiệm hệ \(\left\{{}\begin{matrix}4x-y-5=0\\x-y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\Rightarrow M=\left(2;3\right)\)
\(min=2\sqrt{17}\Leftrightarrow M=\left(2;3\right)\)