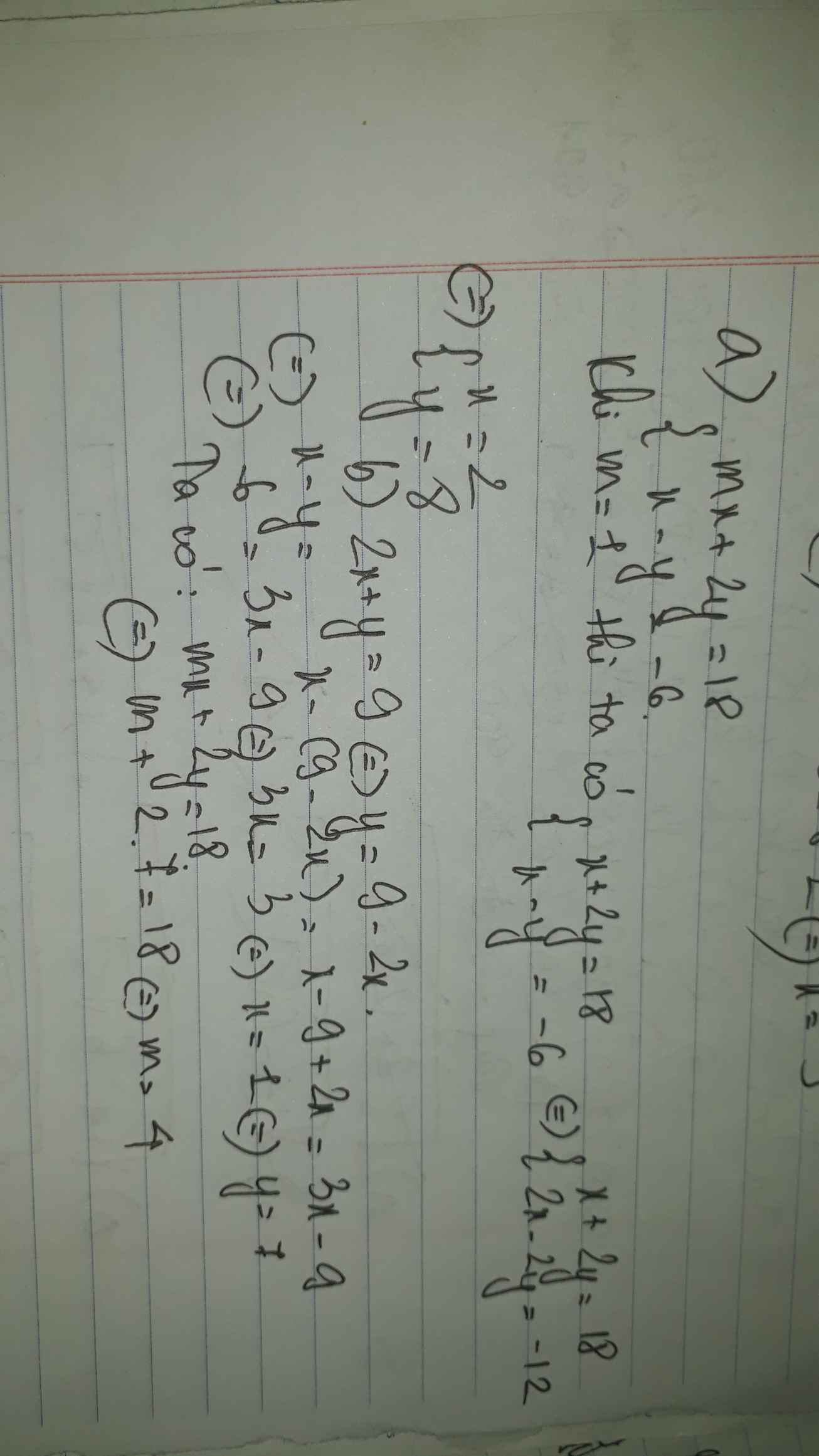a. Với `m=1`, ta có HPT: \(\left\{{}\begin{matrix}x+2y=18\\x-y=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y=-6\\3y=24\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=8\end{matrix}\right.\)
b. Theo đề bài `=>` \(\left\{{}\begin{matrix}mx+2y=18\\x-y=-6\\2x+y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}mx+2y=18\\x=1\\y=7\end{matrix}\right.\)
`=> m=4`
a) Thay m=1 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}x+2y=18\\x-y=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3y=24\\x-y=-6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=8\\x=-6+y=-6+8=2\end{matrix}\right.\)