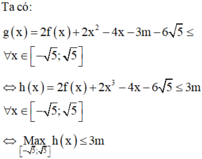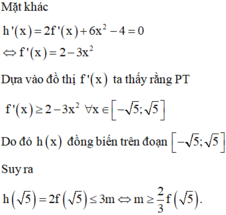Các câu hỏi tương tự
Cho hàm số y f(x) có đồ thị hàm số y f (x) như hình vẽ. Xét hàm số
g
x
2
f
x
+
2
x
3
-
4
x
-
3
m
-
6
5
với m là số thực. Để
g
x
≤
0
,
∀
x
∈
-
5...
Đọc tiếp
Cho hàm số y = f(x) có đồ thị hàm số y = f '(x) như hình vẽ. Xét hàm số g x = 2 f x + 2 x 3 - 4 x - 3 m - 6 5 với m là số thực. Để g x ≤ 0 , ∀ x ∈ - 5 ; 5 thì điều kiện của m là
A. m ≥ 2 3 f 5
B. m ≤ 2 3 f 5
C. m ≤ 2 3 f 0 - 2 5
D. m ≥ 2 3 f - 5 - 4 5
Cho hàm số yf(x). Đồ thị hàm số yf’(x) như hình vẽ. Đặt
g
(
x
)
3
f
(
x
)
-
x
3
+
3
x
-
m
, với m là tham số thực. Điều kiện cần và đủ để bất phương trình g(x)≥0 nghiệm đúng với
∀
x
∈
-
3
;
3...
Đọc tiếp
Cho hàm số y=f(x). Đồ thị hàm số y=f’(x) như hình vẽ. Đặt g ( x ) = 3 f ( x ) - x 3 + 3 x - m , với m là tham số thực. Điều kiện cần và đủ để bất phương trình g(x)≥0 nghiệm đúng với ∀ x ∈ - 3 ; 3 là
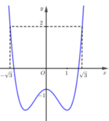
A. m < 3 f 3
B. m > 3 f 3
C. m ≤ 3 f 3
D. m ≥ 3 f 3
Cho hai hàm số
f
(
x
)
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
với
a
≠
0
và g(x)
p
x
2
+
q
x
-
3
c
ó
đồ thị như...
Đọc tiếp
Cho hai hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e với a ≠ 0 và g(x)= p x 2 + q x - 3 c ó đồ thị như hình vẽ bên dưới. Đồ thị hàm số y=f(x) đi qua gốc tọa độ và cắt đồ thị hàm số y=g(x) tại bốn điểm có hoành độ lần lượt là -2;-1;1 và m. Tiếp tuyến của đồ thị hàm số y=f(x)-g(x) tại điểm có hoành độ x=-2 có hệ số góc bằng -15/2. Gọi (H) là hình phẳng giới hạn bởi đồ thị hai hàm số y=f(x) và y=g(x) (phần được tô đậm trong hình vẽ). Diện tích của hình (H) bằng

A. 1553 120
B. 1553 240
C. 1553 60
D. 1553 30
Cho hàm số yf(x) có đạo hàm liên tục trên R và có đồ thị hàm số yf (x) như hình vẽ bên. Xét hàm số g(x)f(x^2-3) và các mệnh đề sau:1. Hàm số g(x) có 3 điểm cực trị.2. Hàm số g(x)đạt cực tiểu tại x 0.3. Hàm số g(x)đạt cực đại tại x 2.4. Hàm số g(x)đồng biến trên khoảng (-2;0).5. Hàm số g(x)nghịch biến trên khoảng (-1;1). Có bao nhiêu mệnh đề đúng trong các mệnh đề trên? A. 1. B. 4. C. 3. D. 2.
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f' (x) như hình vẽ bên. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 1.
B. 4.
C. 3.
D. 2.
Cho hàm số yf(x). Đồ thị hàm số yf’(x) như hình vẽCho bất phương trình
3
.
f
x
≥
x
3
-
3
x
+
m
, (m là tham số thực). Điều kiện cần và đủ để bất phương trình
3
.
f
x
≥
x
3
-
3
x
+
m
đúng với mọi x thuộc đoạn
-...
Đọc tiếp
Cho hàm số y=f(x). Đồ thị hàm số y=f’(x) như hình vẽ
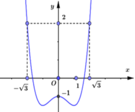
Cho bất phương trình 3 . f x ≥ x 3 - 3 x + m , (m là tham số thực). Điều kiện cần và đủ để bất phương trình 3 . f x ≥ x 3 - 3 x + m đúng với mọi x thuộc đoạn - 3 ; 3 là
A. m ≥ 3 f - 3
B. m ≤ 3 f 3
C. m ≥ 3 f 1
D. m ≤ 3 f 0
Cho hai hàm đa thức y f(x), y g(x) có đồ thị là hai đường cong ở hình vẽ. Biết rằng đồ thị hàm số y f(x) có đúng một điểm cực trị là A, đồ thị hàm số y g(x) có đúng một điểm cực trị là B và
A
B
7
4
.
Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (-5;5) để hàm số
y
f
(
x
)...
Đọc tiếp
Cho hai hàm đa thức y = f(x), y = g(x) có đồ thị là hai đường cong ở hình vẽ. Biết rằng đồ thị hàm số y = f(x) có đúng một điểm cực trị là A, đồ thị hàm số y = g(x) có đúng một điểm cực trị là B và A B = 7 4 . Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (-5;5) để hàm số y = f ( x ) - g ( x ) + m có đúng 5 điểm cực trị?
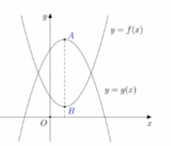
A. 1
B. 3
C. 4
D. 6
Cho hàm số y f(x) có đồ thị hàm số
y
f
x
như hình vẽ:Xét hàm số
g
x
2
f
x
+
2
x
3
−
4
x
−
3
m
−
6
5
với
m
là số thực. Điều kiện cần và đủ để
g
x
≤
0...
Đọc tiếp
Cho hàm số y = f(x) có đồ thị hàm số y = f ' x như hình vẽ:

Xét hàm số g x = 2 f x + 2 x 3 − 4 x − 3 m − 6 5 với m là số thực. Điều kiện cần và đủ để g x ≤ 0 ∀ x ∈ − 5 ; 5 là:
A. m ≥ 2 3 f 5
B. m ≥ 2 3 f − 5
C. m ≥ 2 3 f 0
D. m ≤ 2 3 f 5
Cho hàm số yf(x) liên tục và có đạo hàm trên R. Biết hàm số f’(x) có đồ thị được cho trong hình vẽ. Tìm điều kiện của m để hàm số g(x)f(2019)x – mx +2 đồng biến trên [0;1]
Đọc tiếp
Cho hàm số y=f(x) liên tục và có đạo hàm trên R. Biết hàm số f’(x) có đồ thị được cho trong hình vẽ. Tìm điều kiện của m để hàm số g(x)=f(2019)x – mx +2 đồng biến trên [0;1]
![]()
![]()
![]()
![]()
Cho hàm số yf(x) có đạo hàm liên tục trên , đồ thị hàm số yf’(x) như hình vẽ bên dưới. Cho bất phương trình
f
e
x
+
2
3
e
3
x
-
e
x
-
m
≥
0
; với m là tham số thực. Tìm điều kiện cần và đủ để bất phương trình
f
e...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên , đồ thị hàm số y=f’(x) như hình vẽ bên dưới. Cho bất phương trình f e x + 2 3 e 3 x - e x - m ≥ 0 ; với m là tham số thực. Tìm điều kiện cần và đủ để bất phương trình f e x + 2 3 e 3 x - e x - m ≥ 0 đúng với mọi x ∈ - 2 ; 2
A. m ≤ f e + 2 3 e 3 - e
B. m ≤ f 1 - 1 3
C. m ≤ f 1 e + 2 3 e - 3 - e - 1
D. m ≤ f e 2 + 2 3 e 3 2 - e 2