Bài 2: Giới hạn của hàm số
Các câu hỏi tương tự
Cho hai hàm số yfleft(xright) và ygleft(xright) cùng xác định trên khoảng left(-infty;aright). Dùng định nghĩa chứng minh rằng nếu limlimits_{xrightarrow-infty}fleft(xright)L và limlimits_{xrightarrow-infty}gleft(xright)M thì limlimits_{xrightarrow-infty}fleft(xright).gleft(xright)L.M
Đọc tiếp
Cho hai hàm số \(y=f\left(x\right)\) và \(y=g\left(x\right)\) cùng xác định trên khoảng \(\left(-\infty;a\right)\). Dùng định nghĩa chứng minh rằng nếu \(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=L\) và \(\lim\limits_{x\rightarrow-\infty}g\left(x\right)=M\) thì \(\lim\limits_{x\rightarrow-\infty}f\left(x\right).g\left(x\right)=L.M\)
Cho khoảng K,x_0in K và hàm số yfleft(xright) xác định trên K left{x_0right}
Chứng minh rằng nếu limlimits_{xrightarrow x_0}fleft(xright)+infty thì luôn tồn tại ít nhất một số c thuộc K left{x_0right} sao cho fleft(cright)0
Đọc tiếp
Cho khoảng \(K,x_0\in K\) và hàm số \(y=f\left(x\right)\) xác định trên \(K\)\ \(\left\{x_0\right\}\)
Chứng minh rằng nếu \(\lim\limits_{x\rightarrow x_0}f\left(x\right)=+\infty\) thì luôn tồn tại ít nhất một số c thuộc \(K\)\ \(\left\{x_0\right\}\) sao cho \(f\left(c\right)>0\)
\(\lim\limits_{x\rightarrow-\infty}\left(3x^3+5x^2-9\sqrt{2}x-2017\right)\)
\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{x^2+x+1}-\sqrt[3]{2x^3+x-1}\right)\)
\(\lim\limits_{x\rightarrow-\infty}\left(x-\sqrt{x^2+x+1}\right)\)
\(\lim\limits_{x\rightarrow-\infty}\left(\sqrt[3]{x^3+x^2+1}+\sqrt{x^2+x+1}\right)\)
Cho hàm số fleft(xright)dfrac{x+2}{x^2-9} có đồ thị như hình trên (Hình 53)
a) Quan sát đồ thị và nêu nhận xét về giá trị hàm số đã cho khi xrightarrow-infty, xrightarrow3^-,xrightarrow-3^+
b) Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau :
* limlimits_{xrightarrow-infty}fleft(xright) với fleft(xright) được xét trên khoảng left(-infty;-3right)
* limlimits_{xrightarrow3^-}fleft(xright) với fleft(xright) được xét trên khoảng left(-3;3right)
* limlimits_{xrightarrow-3^+}fleft(xr...
Đọc tiếp
Cho hàm số \(f\left(x\right)=\dfrac{x+2}{x^2-9}\) có đồ thị như hình trên (Hình 53)
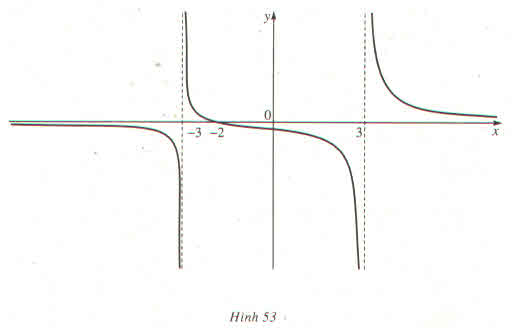
a) Quan sát đồ thị và nêu nhận xét về giá trị hàm số đã cho khi \(x\rightarrow-\infty\), \(x\rightarrow3^-,x\rightarrow-3^+\)
b) Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau :
* \(\lim\limits_{x\rightarrow-\infty}f\left(x\right)\) với \(f\left(x\right)\) được xét trên khoảng \(\left(-\infty;-3\right)\)
* \(\lim\limits_{x\rightarrow3^-}f\left(x\right)\) với \(f\left(x\right)\) được xét trên khoảng \(\left(-3;3\right)\)
* \(\lim\limits_{x\rightarrow-3^+}f\left(x\right)\) với \(f\left(x\right)\) được xét trên khoảng \(\left(-3;3\right)\)Bài 1
a. limlimits_{xrightarrow-infty}frac{sqrt{4x^2}+1}{3x-1}
b. limlimits_{xrightarrow+infty}frac{sqrt{9x^2+x+1}-sqrt{4x^2+2x+1}}{x+1}
c. limlimits_{xrightarrow+infty}frac{sqrt{x+2x+3}+4x+1}{sqrt{4x^2+1}+2-x}
d. limlimits_{xrightarrow+infty}frac{3x-2sqrt{x}+sqrt{x^4-5x}}{2x^2+4x-5}
Bài 2
a. limlimits_{xrightarrow-infty}frac{2x+1}{x-1}
b. limlimits_{xrightarrow-infty}frac{2x^3+3}{x^3-2x^2+1}
c. limlimits_{xrightarrow+infty}frac{left(3x^2+1right)left(5x+3right)}{left(2x^3-1r...
Đọc tiếp
Bài 1
a. \(\lim\limits_{x\rightarrow-\infty}\frac{\sqrt{4x^2}+1}{3x-1}\)
b. \(\lim\limits_{x\rightarrow+\infty}\frac{\sqrt{9x^2+x+1}-\sqrt{4x^2+2x+1}}{x+1}\)
c. \(\lim\limits_{x\rightarrow+\infty}\frac{\sqrt{x+2x+3}+4x+1}{\sqrt{4x^2+1}+2-x}\)
d. \(\lim\limits_{x\rightarrow+\infty}\frac{3x-2\sqrt{x}+\sqrt{x^4-5x}}{2x^2+4x-5}\)
Bài 2
a. \(\lim\limits_{x\rightarrow-\infty}\frac{2x+1}{x-1}\)
b. \(\lim\limits_{x\rightarrow-\infty}\frac{2x^3+3}{x^3-2x^2+1}\)
c. \(\lim\limits_{x\rightarrow+\infty}\frac{\left(3x^2+1\right)\left(5x+3\right)}{\left(2x^3-1\right)\left(x+4\right)}\)
a. \(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{x+\sqrt{x+\sqrt{x}}}-\sqrt{x-\sqrt{x-\sqrt{x}}}\right)\)
b. \(\lim\limits_{x\rightarrow+\infty}x\left(\sqrt{x^2+2x}-2\sqrt{x^2+x}+x\right)\)
c. \(\lim\limits_{x\rightarrow+\infty}\left(\sqrt[3]{x^3+3x^2}-\sqrt{x^2-2x}\right)\)
Tính :
a) \(\lim\limits_{x\rightarrow+\infty}\left(x^4-x^2+x-1\right)\)
b) \(\lim\limits_{x\rightarrow-\infty}\left(-2x^3+3x^2-5\right)\)
c) \(\lim\limits_{x\rightarrow-\infty}\sqrt{x^2-2x+5}\)
d) \(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x^2+1}+x}{5-2x}\)
1, Tính:
a, \(\lim\limits_{x\rightarrow-2}\dfrac{x^3+2x^2}{\sqrt{x^2+4x+4}}\)
b, \(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{x+\sqrt{x+1}}-\sqrt{x}\right)\)
c, \(\lim\limits_{x\rightarrow-\infty}\left(\sqrt{x^2-x}+1+\sqrt[3]{x^3+2}\right)\)
Bài 1
a. limlimits_{xrightarrow-infty}left(sqrt[3]{x^3-x^2}-xright)
b. limlimits_{xrightarrow+infty}left(sqrt[3]{x^3+5x^2}-sqrt[3]{x^3+8x}right)
c. limlimits_{xrightarrow+infty}left(sqrt[3]{x^3+1}-xright)
Bài 2
a. limlimits_{xrightarrow1^-}left(frac{2}{x^2-1}-frac{1}{x-1}right)
b. limlimits_{xrightarrow1^+}left(frac{1}{1-x}-frac{3}{1-x^3}right)
c. limlimits_{xrightarrow2^+}left(frac{1}{x^2-3x+2}-frac{1}{x^2-5x+6}right)
Đọc tiếp
Bài 1
a. \(\lim\limits_{x\rightarrow-\infty}\left(\sqrt[3]{x^3-x^2}-x\right)\)
b. \(\lim\limits_{x\rightarrow+\infty}\left(\sqrt[3]{x^3+5x^2}-\sqrt[3]{x^3+8x}\right)\)
c. \(\lim\limits_{x\rightarrow+\infty}\left(\sqrt[3]{x^3+1}-x\right)\)
Bài 2
a. \(\lim\limits_{x\rightarrow1^-}\left(\frac{2}{x^2-1}-\frac{1}{x-1}\right)\)
b. \(\lim\limits_{x\rightarrow1^+}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)\)
c. \(\lim\limits_{x\rightarrow2^+}\left(\frac{1}{x^2-3x+2}-\frac{1}{x^2-5x+6}\right)\)