Đáp án A
Phương pháp:
Nếu l i m x → + ∞ y = a hoặc l i m x → - ∞ y = a thì y = a là TCN của đồ thị hàm số y = f(x)
Nếu l i m x → b + y = ∞ hoặc l i m x → b - y = ∞ thì x = b là TCĐ của đồ thị hàm số y = f(x)
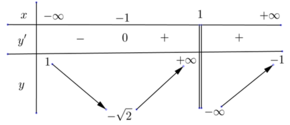
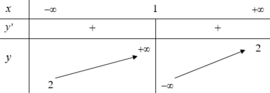
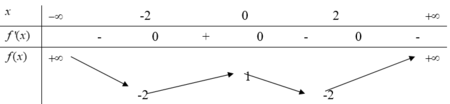
Cách giải: Do hàm số liên tục trên R nên đồ thị hàm số không có TCĐ.
l i m x → - ∞ f ( x ) = 0 ; l i m x → + ∞ f ( x ) = 1 → y = 0 và y = 1 là 2 đường TCN của đồ thị hàm số.