\(y=f\left(x\right)=2x^3-9x^2+12x+m^2\)
\(f'\left(x\right)=6x^2-18x+12\)
\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
bbt:
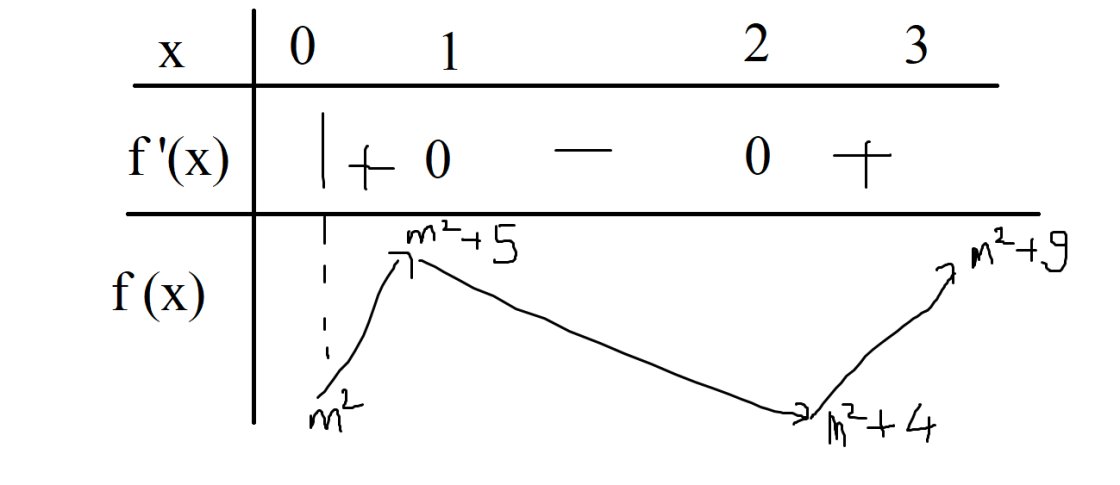
Theo bbt thì \(min_{\left[0,3\right]}f\left(x\right)=f\left(0\right)=m^2\Rightarrow m^2=0\Rightarrow m=0\)
Vậy chỉ có một giá trị m thỏa đề






