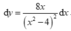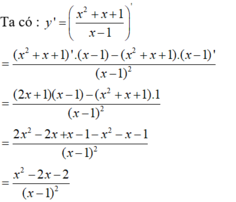
- Do đó, vi phân của hàm số đã cho là:
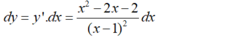
Chọn D.
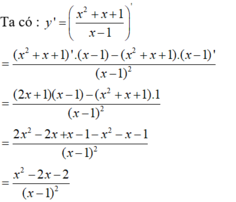
- Do đó, vi phân của hàm số đã cho là:
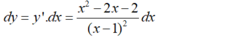
Chọn D.
xác định đường tiệm cận đứng của đồ thị hàm số sau
a) \(y=\dfrac{\sqrt{x-2}+1}{x^2-3x+2}\)
b) \(y=\dfrac{\sqrt{5+x}-1}{x^2+4x}\)
c) \(y=\dfrac{5x+1-\sqrt{x+1}}{x^2+2x}\)
d) \(y=\dfrac{\sqrt{4x^2-1}+3x^2+2}{x^2-x}\)
Tinh đao hàm của các hàm số
a (m + n/x^2)^4
b y =(3x-2)^11.(1-2x)^21
c y = căn của 2x-1/2x+1
d y = x . căn của x^2 +4
xác định đường tiệm cận đứng của đồ thị hàm số sau
a) \(y=\dfrac{x+3}{x^2-9}\)
b) \(y=\dfrac{x-5}{x^2-25}\)
c) \(y=\dfrac{x^2-4x+3}{x^2-1}\)
d) \(y=\dfrac{x^2-3x-4}{x^2-2x-3}\)
Tính đạo hàm của các hàm số sau
a) y= căn ( 3x-2/x+1 )
b)y=1/căn (2x^2+x+13)
c)y=căn(x^2+x+9)/6x-1
d)y=sin3x/cosx cos2x
e)y=căn(1+2xcosx)
f)y=3tanx-cotx/cotx +tanx
g)y=x^2+x-1/x-2 h)y=(x+1)cotx
trong các hàm số sau đây , hàm số nào không tuần hoàn
a. y= x.sin x
b. y= cos 2x
c. y=sin(x-x/2)
d. y=1/sin2x
1. Mệnh đề nào dưới đây sai ?
A. Hàm số y = tan x là hàm số lẻ. B. Hàm số y = sin x là hàm số lẻ
C. Hàm số y = Cot x là hàm số lẻ D. Hàm số y = Cos x là hàm số lẻ
2. Hàm số nào sau đây là hàm số lẻ?
A. y = Cos3x B. y = Sinx + Cos3x
C. y = Sinx + Tan3x D. Tan2x
3. Trong các hàm số sau, hàm số nào là hàm số chẵn
A. y = Cos2x B. y = Cot2x
C. y = tan2x D. y = sin2x
4. Trong các hàm số sau, hàm số nào là hàm số lẻ?
A. y = Sinx Cos3x
B. y = Cosx + Sin2x
C. y = Cosx + Sinx
D. y = - Cosx
5. Hàm số nào là hàm số chẵn ?
A. y = Cosx
B. y = Sin x/2
C. y = tan2x
D. y = Cotx
tìm tập xác định của hàm số
a) \(y=log_2\left(x^2-16\right)\)
b) \(y=log_3\left(x^2-2x+1\right)\)
c) \(y=log_2\left(2-x\right)\left(x+1\right)\)
d) \(y=log\left(x^2-1\right)\left(X+5\right)\)
tìm tập xác định của hàm số sau
a) \(y=log_2\left(2x+6\right)\)
b) \(y=log_2\left(x-6\right)\)
c) \(y=log_3\dfrac{1}{2-x}\)
d) \(y=log_2\left(x-6\right)\left(x+2\right)\)
Đạo hàm của hàm số \(y=\left(x^2-\dfrac{2}{x}\right)^3\)là:
A. \(y'=6\left(x+\dfrac{1}{x^2}\right)\left(x^2-\dfrac{2}{x}\right)^2\)
B. \(y'=3\left(x^2-\dfrac{2}{x}\right)^2\)
C. \(y'=6\left(x-\dfrac{1}{x^2}\right)\left(x^2-\dfrac{2}{x}\right)^2\)
D. \(y'=6\left(x-\dfrac{1}{x}\right)\left(x^2-\dfrac{2}{x}\right)^2\)
Vi phân của hàm số y = x - 1 2 x + 1 + 1 2 x + 1 : x - 2 x + 2 + x - 2 + x - 2 x 2 - 4 - x + 2 2 trên tập xác định là
A. ![]()
B. ![]()
C. ![]()
D.