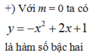
Hàm số y = - x 2 + 2 x + không nghịch biến trên ℝ ⇒ m = 0 không thỏa mãn
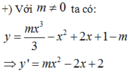
Để hàm số nghịch biến trên ℝ thì
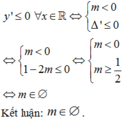
Chọn: D
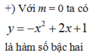
Hàm số y = - x 2 + 2 x + không nghịch biến trên ℝ ⇒ m = 0 không thỏa mãn
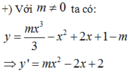
Để hàm số nghịch biến trên ℝ thì
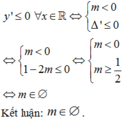
Chọn: D
Cho hàm số f(x)=3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số y = f 3 ( x ) - 3 mf 2 ( x ) + 3 ( m 2 - 4 ) f ( x ) - m nghịch biến trên khoảng (0;π/2). Số tập con của S bằng
A. 1
B. 2.
C. 4.
D. 16.
Cho hàm số y = 1 3 x 3 + 2 x 2 + ( m + 2 ) x - m . Tìm tập hợp S tất cả các giá trị thực của tham số m để hàm số đồng biến trên ℝ
A. S = ( - ∞ ; 2 ]
B. S = ( - ∞ ; 2 )
C. S = [ 2 ; + ∞ )
D. S = ( 2 ; + ∞ )
Biết rằng S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số y = x 3 - 3(m-1) x 2 + 3m(m+2)x nghịch biến trên đoạn [0;1]. Tính tổng các phần tử của S?
A. S = 0.
B. S = 1.
C. S = -2.
D. S = -1.
Cho hàm số y = sin 3 x − 3 sin 2 xcosx + 1 − m sinxcos 2 x + 2 cos 3 x cos 3 x . Tập hợp tất cả các giá trị của m để hàm số nghịch biến trên 0 ; π 4 là
A. − 2 ; + ∞ .
B. − ∞ ; 3 .
C. − 2 ; 3 .
D. 1 ; + ∞ .
Cho hàm số y = sin 3 x − 3 sin 2 xcosx + 1 − m sinxcos 2 x + 2 cos 3 x cos 3 x . Tập hợp tất cả các giá trị của m để hàm số nghịch biến trên 0 ; π 4 là
A. − 2 ; + ∞ .
B. − ∞ ; 3 .
C. − 2 ; 3 .
D. 1 ; + ∞ .
Một học sinh giải bài toán “Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m x 3 + m x 2 + m − 2 x + 10 đồng biến trên i” theo các bước như sau:
Bước 1: Hàm số xác định trên i, và y ' = 3 m x 2 + 2 m x + m − 2
Bước 2: Yêu cầu bài toán tương đương với y ' > 0, ∀ x ∈ ℝ ⇔ 3 m x 2 + 2 m x + m − 2 > 0, ∀ x ∈ ℝ
Bước 3: ⇔ a = 3 m > 0 Δ ' = 6 m − 2 m 2 < 0 ⇔ m < 0 m > 3 m > 0
Bước 4: ⇔ m > 3. Vậy m>3
Hỏi học sinh này đã bắt đầu sai ở bước nào?
A. Bước 2
B. Bước 3
C. Bước 1
D. Bước 4
Cho hàm số y = f x xác định, liên tục và có đạo hàm trên đoạn a , b . Xét các khẳng định sau:
1. Hàm số f x đồng biến trên a ; b thì f ' x > 0 , ∀ x ∈ a ; b
2. Giả sử f a > f c > f b , ∀ x ∈ a ; b suy ra hàm số nghịch biến trên a ; b
3. Giả sử phương trình f ' x = 0 có nghiệm là x = m khi đó nếu hàm số y = f x đồng biến trên m ; b thì hàm số y = f x nghịch biến trên a , m
4. Nếu f ' x ≥ 0 , ∀ x ∈ a ; b , thì hàm số đồng biến trên a ; b
Số khẳng định đúng trong các khẳng định trên là
A. 1
B. 0
C. 3
D. 2
Tìm tất cả các giá trị tham số m để hàm số y = 1 3 ( m - 1 ) x 3 - ( m - 1 ) x 2 - x + 1 nghịch biến trên ℝ
A. m ≥ 1 m ≤ 0
B. 0 ≤ m ≤ 1
C. m ≥ 1 m ≤ - 3
D. - 3 ≤ m ≤ 1
Cho hàm số f x có đạo hàm trên ℝ thỏa mãn f x + h - f x - h ≤ h 2 , ∀ x ∈ ℝ , ∀ h > 0 .Đặt g x = x + f ' x 2019 + x + f ' x 29 - m - m 4 - 29 m 2 + 100 sin 2 x - 1 , m là tham số nguyên mà m < 27. Gọi S là tập hợp tất cả các giá trị nguyên của m sao cho hàm số g (x) đạt cực tiểu tại x = 0. Tính tổng bình phương các phần tử của S.
A. 108
B. 58
C. 100
D. 50