Chọn A.
Phương pháp : Sử dụng đạo hàm và đặc trưng cực trị hàm số đa thức bậc ba.
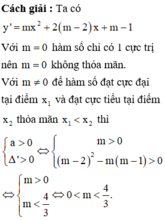
Chọn A.
Phương pháp : Sử dụng đạo hàm và đặc trưng cực trị hàm số đa thức bậc ba.
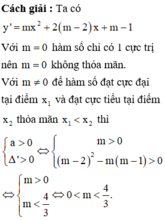
Tìm tất cả các giá trị thực của tham số m để hàm số y = − 2 x 3 + 3 m x 2 − 1 đạt cực tiểu tại x= 0.
A. m > 0
B. m > 1 2
C. m<0
D. m < 1 2
Tìm tất cả các giá trị của tham số thực m để hàm số y = 1 3 x 3 − m x 2 + m 2 − m + 1 x + 1 đạt cực đại tại điểm x=1
A.m=2
B.m=3
C.m= -1
D. m=0
Tất cả các giá trị thực của tham số m để hàm số y = x 5 5 – m x 4 4 + 2 đạt cực đại tại x=0 là
A. m > 0
B. m < 0
C. mÎR
D. Không tồn tại m
Tìm tất cả các giá trị thực của tham số m để hàm số y = 1 3 x 3 − 1 2 m 2 + 1 x 2 + 3 m − 2 x + m đạt cực đại tại điểm x=1
A. m=-1
B. m=2
C. m=1
D. m=-2
Tìm tất cả các giá trị của tham số thực m để hàm số y = − x 3 − 2 x 2 + m x + 1 đạt cực tiểu tại điểm x = -1
A. m < -1
B. m ≠ − 1
C. m = -1
D. m > -1
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 4 − 2 m + 1 x 2 + m 2 − 1 đạt cực tiểu tại x = 0.
A. m<-1
B. m=-1
C. m ≤ − 1.
D. m ≤ − 1 m ≥ 1
Tìm tất cả các giá trị thực của tham số m để hàm số y = − x 3 + 2 m x 2 − m 2 x − 2 đạt cực tiểu tại x = 1
A. m = − 1 m = 3
B. m = 1 m = 3
C. m = 3
D. m = 11
Tìm tất cả các giá trị thực của tham số m để hàm số y = − x 3 + 2 m x 2 − m 2 x − 2 đạt cực tiểu tại x = 1.
A. m = − 1 m = 3
B. m = 1 m = 3
C. m = 3
D. m = 3
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 4 + m x 2 đạt cực tiểu tại x = 0
A. m = 0.
B. m > 0.
C. m ³ 0.
D. m £ 0.