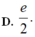Các câu hỏi tương tự
Cho hàm số f(x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;2] thoả mãn f(0) 3; f(2) 12 và
∫
0
2
(
f
(
x
)
)
2
f
(
x
)
d
x...
Đọc tiếp
Cho hàm số f(x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;2] thoả mãn f(0) = 3; f(2) = 12 và ∫ 0 2 ( f ' ( x ) ) 2 f ( x ) d x = 6 Tính f(1)
A. 27/4
B. 25/4
C. 9/2
D. 15/4
Cho hàm số f(x) có đạo hàm dương, liên tục trên đoạn [0;1] thỏa mãn điều kiện f(0)1 và
3
∫
0
1
f
(
x
)
.
f
(
x
)
2
+...
Đọc tiếp
Cho hàm số f(x) có đạo hàm dương, liên tục trên đoạn [0;1] thỏa mãn điều kiện f(0)=1 và 3 ∫ 0 1 f ' ( x ) . f ( x ) 2 + 1 9 d x ≤ 2 ∫ 0 1 f ' ( x ) . f ( x ) d x Tính ∫ 0 1 f ( x ) 3 d x
A. 3/2
B. 5/4
C. 5/6
D. 7/6
chỉ mik cách lập nhóm nhaTrích một số bài toán trong đề:+ Trên mặt phẳng phức, tập hợp điểm biểu diễn cho số phức z thỏa mãn điều kiện /z/ 2 là:A. Đường tròn tâm O, bán kính R 2B. Đường tròn tâm O, bán kính R 4C. Đường tròn tâm O, bán kính R 1/2D. Đường tròn tâm O , bán kính R căn 2+ Cho hàm số y f(x) xác định, liên tục trên R và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây đúng?A. Hàm số y f(x) có giá trị cực đại bằng 0B. Giá trị lớn nhất của hàm số y f(x) trên tập R là 1C. Hà...
Đọc tiếp
chỉ mik cách lập nhóm nha
Trích một số bài toán trong đề:
+ Trên mặt phẳng phức, tập hợp điểm biểu diễn cho số phức z thỏa mãn điều kiện /z/ = 2 là:
A. Đường tròn tâm O, bán kính R = 2
B. Đường tròn tâm O, bán kính R = 4
C. Đường tròn tâm O, bán kính R = 1/2
D. Đường tròn tâm O , bán kính R = căn 2
+ Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây đúng?
A. Hàm số y = f(x) có giá trị cực đại bằng 0
B. Giá trị lớn nhất của hàm số y = f(x) trên tập R là 1
C. Hàm số y = f(x) đạt cực đại tại x = 0 và cực tiểu tại x = -1
D. Hàm số y = f(x) có đúng một cực trị
+ Tìm phần thực của số phức (2 + 3i).i^10
Cho hàm số liên tục trên khoảng (a;b) và
x
0
∈
(
a
;
b
)
.
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?(1) Hàm số đạt cực trị tại điểm
x
0
khi và chỉ khi
f
(
x
0
)
0
.
(2) Nếu hàm số
y
f
(
x
)
có đạo hàm và có đạo...
Đọc tiếp
Cho hàm số liên tục trên khoảng (a;b) và x 0 ∈ ( a ; b ) . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' ( x 0 ) = 0 .
(2) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = f ' ' ( x 0 ) = 0 thì điểm x 0 không phải là điểm cực trị của hàm số y = f ( x ) .
(3) Nếu f'(x) đổi dấu khi x qua điểm x 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
(4) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = 0 , f ' ' ( x 0 ) > 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
A. 1
B. 2
C. 0
D. 3
Cho hàm số f(x) có đạo hàm f(x) liên tục trên R và thỏa mãn
f
(
x
)
∈
[
-
1
;
1
]
với
∀
x
∈
(
0
;
2
)
Biết f(0) f(2) 1 Đặt
I
∫
0
2
f
(
x
)
d
x
phát bi...
Đọc tiếp
Cho hàm số f(x) có đạo hàm f'(x) liên tục trên R và thỏa mãn f ' ( x ) ∈ [ - 1 ; 1 ] với ∀ x ∈ ( 0 ; 2 ) Biết f(0) = f(2) = 1 Đặt I = ∫ 0 2 f ( x ) d x phát biểu dưới đây là ĐÚNG ?
![]()
![]()
![]()
![]()
Cho hàm số f(x) thỏa mãn các điều kiện f(1) 2,
f
x
≠
0
∀
x
0
và
x
2
+
1
2
f...
Đọc tiếp
Cho hàm số f(x) thỏa mãn các điều kiện f(1) = 2, f x ≠ 0 ∀ x > 0 và x 2 + 1 2 f ' x = f x 2 x 2 - 1 với mọi x>0. Giá trị của f(2) bằng
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số f(x) liên tục trên R thỏa mãn điều kiện:
f
(
0
)
2
3
,
f
(
x
)
0
,
∀
x
∈
ℝ
và
f
(
x
)
.
f
(
x
)
(
2
x
+
1
)
1
+
f...
Đọc tiếp
Cho hàm số f(x) liên tục trên R thỏa mãn điều kiện: f ( 0 ) = 2 3 , f ( x ) > 0 , ∀ x ∈ ℝ và f ( x ) . f ' ( x ) = ( 2 x + 1 ) 1 + f 2 ( x ) , ∀ x ∈ ℝ . Khi đó giá trị f(1) bằng:
![]()
![]()
![]()
![]()
Cho hàm số yf(x) liên tục trên
(
0
;
+
∞
)
và thỏa mãn 2xf(x)+f(x)
3
x
2
x
biết f(1)
1
2
. Gía trị f(2) bằng
Đọc tiếp
Cho hàm số y=f(x) liên tục trên ( 0 ; + ∞ ) và thỏa mãn 2xf'(x)+f(x)= 3 x 2 x biết f(1)= 1 2 . Gía trị f(2) bằng
![]()
![]()
![]()
![]()
Cho hàm số f(x) có đạo hàm liên tục trên [0;1] thỏa mãn điều kiện:
∫
0
1
f
(
x
)
2
d
x
∫
0
1
(
x
+
1
)
e
x
f
(...
Đọc tiếp
Cho hàm số f(x) có đạo hàm liên tục trên [0;1] thỏa mãn điều kiện: ∫ 0 1 f ' ( x ) 2 d x = ∫ 0 1 ( x + 1 ) e x f ( x ) d x = e x - 1 4 và f(1)=0 Tính giá trị tích phân
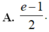
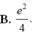
![]()