Chọn C

Do đó diện tích hình phẳng giới hạn bởi
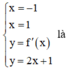
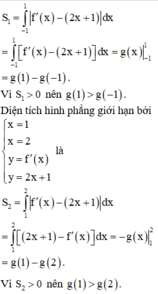
Chọn C
Chọn C


Do đó diện tích hình phẳng giới hạn bởi
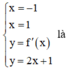
Chọn C
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f' (x) như hình vẽ bên. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 1.
B. 4.
C. 3.
D. 2.
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có
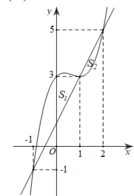
đồ thị y=f'(x) như hình vẽ bên. Đặt g ( x ) = f ( x ) - x 2 2 biết rằng
đồ thị của hàm g(x) luôn cắt trục hoành tại 4 điểm phân biệt.
Mệnh đề nào dưới đây đúng

A. g ( 0 ) > 0 g ( 1 ) < 0 g ( - 2 ) g ( 1 ) > 0
B. g ( 0 ) > 0 g ( 1 ) > 0 g ( - 2 ) g ( 1 ) < 0
C. g ( 1 ) < 0 g ( 0 ) > 0
D. g ( 0 ) > 0 g ( - 2 ) < 0
Cho hàm sốy =f(x), y =g(x)liên tục trên ℝ và có đồ thị các đạo hàm (đồ thị y =g’(x) là đường đậm hơn) như hình vẽ
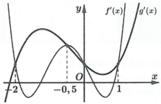
Hàm số h(x) =f(x-1) –g(x-1) nghịch biến trên khoảng nào dưới đây?
A. (1/2;1).
B. (-1;1/2).
C. (1;+∞).
D. (2;+∞)
Cho hàm số y=f(x) có đạo hàm trên R. Đường cong hình vẽ bên là đồ thị hàm số y=f '(x) (Hàm số y=f '(x) liên tục trên R. Xét hàm số g ( x ) = f ( x 2 - 2 ) . Mệnh đề nào dưới đây là sai?
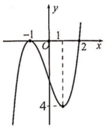
A. Hàm số y=g(x) đồng biến trên khoảng (-2;-1)
B. Hàm số y=g(x) đồng biến trên khoảng 2 ; + ∞
C. Hàm số y=g(x) nghịch biến trên khoảng (-1;0)
D. Hàm số y=g(x) nghịch biến trên khoảng (0;2)
Cho hàm số y=f(x) có đạo hàm trên R. Đồ thị của hàm số y=f’(x) như hình vẽ bên, hàm số y = g ( x ) = f ( x ) + 1 2 x 2 + x + 1 . Mệnh đề nào dưới đây là sai?
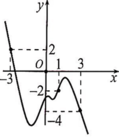
A. Hàm số y=g(x) đồng biến trên khoảng (-∞;-3)
B. Hàm số y=g(x) có 3 cực trị
C. Hàm số y=g(x)đặt cực đại tại x=3
D. Hàm số y=g(x)đặt cực đại tại x=-3
Cho hàm số y=f(x) có đạo hàm trên R Đồ thị hàm số y=f '(x) như hình vẽ bên. Hàm số y = g ( x ) = f ( x ) - 1 3 x 3 - 3 4 x 2 + 3 2 x + 1 Mệnh đề nào dưới đây là sai?
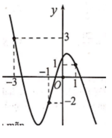
A. Hàm số y=g(x) nghịch biến trên khoảng (-3;-1)
B. Đồ thị hàm số g(x) có 3 điểm cực trị
C. Đồ thị hàm số g(x) có 1 điểm cực trị
D. Hàm số g(x) đạt cực tiểu tại x=-1
Cho hàm số y = f(x) liên tục trên R. Biết đồ thị hàm số y = f’(x) được cho bởi hình vẽ bên, xét hàm số y = g x = f x - x 2 2 . Hỏi trong các mệnh đề sau có bao nhiêu mệnh đề đúng?
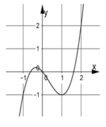
(I) Số điểm cực tiểu của hàm số g(x) là 2.
(II) Hàm số g(x) đồng biến trên khoảng (-1;2).
(III) Giá trị nhỏ nhất của hàm số là g(-1).
(IV) Cực đại của hàm số g(x) là 0.
A. 0
B. 1
C. 2
D. 3
Cho hàm số f(x) có đạo hàm trên R và có đồ thị hàm y = f'(x) như hình vẽ. Xét hàm số g ( x ) = f ( x 2 - 2 ) . Mệnh đề nào dưới đây sai?
A . H à m s ố g ( x ) đ ồ n g b i ế n t r ê n ( 2 ; + ∞ ) .
B . H à m s ố g ( x ) n g h ị c h b i ế n t r ê n ( - 1 ; 0 ) .
C . H à m s ố g ( x ) n g h ị c h b i ế n t r ê n ( 0 ; 2 ) .
D . H à m s ố g ( x ) n g h ị c h b i ế n t r ê n ( - ∞ ; - 2 ) .
Hàm số y = f(x) có đồ thị y = f'(x) như hình vẽ.
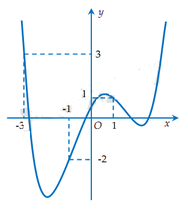
Xét hàm số:
g ( x ) = f ( x ) - 1 3 x 3 - 3 4 x 2 + 3 2 x + 2017
Trong các mệnh đề dưới đây:
(I) g(0) < g(1)
(II) m i n x ∈ - 3 ; 1 g ( x ) = g ( - 1 )
(III) Hàm số g(x) nghịch biến trên (-3;-1)
(IV) m a x x ∈ - 3 ; 1 g ( x ) = m a x g ( - 3 ) , g ( 1 )
Số mệnh đề đúng là:
A. 2
B. 1
C. 3
D. 4
Cho hàm số y=f(x) có đạo hàm, liên tục trên đoạn [-3;3] và đồ thị hàm số y=f' (x) như hình vẽ bên. Biết f(1)=6 và g(x)=f(x)- ( x + 1 ) 2 2 .
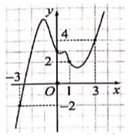
Kết luận nào sau đây là đúng
A. Phương trình g(x)=0 có đúng hai nghiệm thuộc [-3;3].
B. Phương trình g(x)=0 có đúng một nghiệm thuộc [-3;3].
C. Phương trình g(x)=0 không có nghiệm thuộc [-3;3].
D. Phương trình g(x)=0 có đúng ba nghiệm thuộc [-3;3].